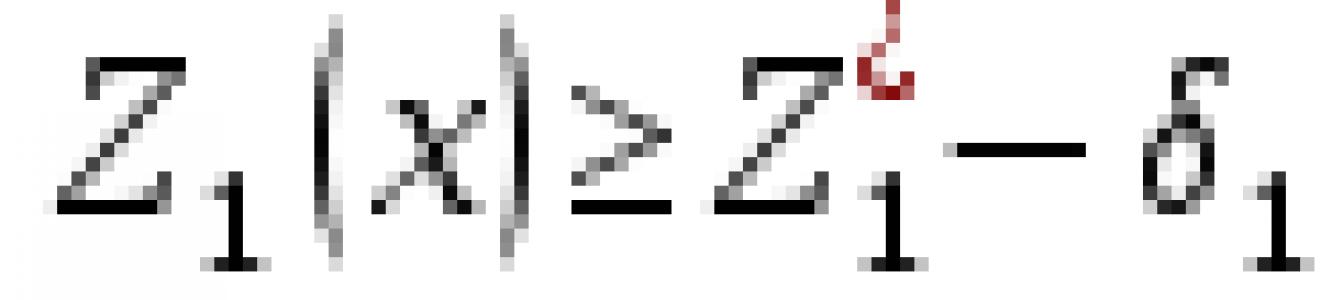1. Расположить критерии по убыванию их значимости.
2. Решить задачу по первому критерию () 1 f x , то есть отыскать
субоптимальное
* решение () . 1
1 f Х = F
* Субоптимальное решение – оптимальное решение по одной из частных целевых функ-
3. Сделать «уступку» по первому критерию, т. е. уменьшить
величину F1 до значения 1 1,
1 F = k F 0 1 1 £ k £ .
4. Ввести в модель дополнительное ограничение
f1 (x) ³ k1F1 = F1 .
5. Решить задачу по второму критерию () 2 f x , т. е. найти су-
боптимальное решение () opt
f2 Х ** = F2.
6. Сделать уступку по второму критерию
2 F = k F 0 1 2 £ k £ .
7. Ввести в задачу дополнительное ограничение
f 2 (x) ³ k2F2 = F2 .
8. Решить задачу по третьему критерию () 3 f x
3 f (Х) = F и т. д.
Субоптимальный план, найденный при решении последней
задачи, является оптимальным компромиссным планом в данной
схеме компромисса.
Ниже на рис. 6.2. приводится наглядная графическая иллюст-
рация данного метода для случая трех целевых функций. Метод
последовательных уступок, являясь чрезвычайно простым и по-
нятным в реализации, обладает, тем не менее, целым рядом недос-
татков, основными из которых являются:
1. Сложность и субъективизм в ранжировании критериев.
2. Субъективизм в задании величин уступок.
3. Степени достижения оптимума (безусловного) по всем
критериям, кроме первого, неопределены. Рассчитать их можно,
лишь решив исходные модели по соответствующим целевым
функциям (еще (S -1) задач) на глобальный оптимум.
** Обращаем внимание читателей на то, что для всех целевых функций, начиная со вто-
рой, оптимальные решения являются условными (в условиях сделанных ранее уступок).
у с т
к о м п р X
Рис. 6.2. Графическая иллюстрация метода последовательных
уступок
4. Поскольку уступка по последнему критерию не делается,
степень достижения оптимума по нему может оказаться совер-
шенно неудовлетворительной. Для «исправления» плана в этом
случае все расчеты должны быть повторены с другими (причем не
гарантирующими нужных окончательных результатов) коэффици-
ентами уступок.
Метод минимизации суммы относительных степеней
достижения цели
Общий вид модели, формализующей данную схему компро-
мисса, будет следующим:
- + - + +
F f x ()
при g x b i i i () £ ," ,
где s F – лучшее, оптимальное _______значение целевой функции s (s =1,S);
f (x) s – текущее значение целевой функции s (s =1,S).
* Данная схема компромисса представляет собой по существу формализованную
интерпретацию основного закона социализма, сформулированного И. Сталиным: «Обес-
печение максимального удовлетворения постоянно растущих материальных и культур-
ных потребностей всего общества путем непрерывного роста и совершенствования со-
циалистического производства на базе высшей техники» (Сталин И. Экономические
проблемы социализма в СССР. – М.: Госполитиздат, 1952).
Основным недостатком данной схемы является взаимоком-
пенсация влияния локальных целевых функций (показателей) на
целевую функцию глобальной модели.
Для устранения данного недостатка в модель должны быть
добавлены дополнительные ограничения, «следящие» за тем, что-
бы по определенному набору локальных целевых показателей не
были получены их недопустимые минимальные уровни.
Метод минимизации равных относительных степеней достиже-
ния цели
Если под компромиссным решением понимать такой план,
который по каждому целевому показателю обеспечивает одинако-
вые относительные отклонения от оптимальных решений, то соот-
ветствующая математическая модель, позволяющая найти это ре-
шение, будет иметь вид
- = - = =
F f x ()
при g x b i i i () £ ," .
Читателю предлагается самостоятельно привести модель к
линейному виду, считая, что целевые функции и функции затрат
всех ресурсов линейны.
Недостатки метода:
1. Уравнительный характер искомого компромиссного плана.
2. Наихудший (по степени достижения цели) показатель оп-
ределяет результаты по всем остальным компонентам целевой
вектор-функции.
Метод максимизации минимальной относительной степени дос-
тижения цели
Свободным от недостатков рассмотренных выше методов яв-
ляется метод, в котором компромисс формализуется как поиск ре-
шения, максимизирующего по всем показателям относительную
минимальную степень достижения цели.
Рассмотрим эту схему компромисса более подробно.
I этап. Все критерии делаются «однонаправленными», на-
пример, решаемыми на максимум. Достигается это изменением
знака на обратный в целевых функциях, соответствующих мини-
мизируемым показателям.
Получаем модель
f (x) = { f1(x); f 2 (x); ...; f s (x)}® max
при g x b i i i () £ ," .
II этап. Исходная модель решается по каждой целевой
функции в отдельности, а результаты решения сводятся в таблицу
Целе-
функ-
Оптимальные
планы
Целевые функции
f1(x) f2(x) … fs(x)
f1(x) opt
X1 () opt
f1 X1 () opt
f2 X1 … () opt
f2(x) opt
X 2 () opt
f1 X2 () opt
f2 X2 … () opt
… … … … … …
fs(x) opt
X s () opt
f1 X s () opt
f2 X s … () opt
Fs – max по столбцу F1 F2 … Fs
fs – min по столбцу f1 f2 … fs
Ds = Fs – fs D1 D2 … Ds
III этап. При решении одноцелевых задач «автоматически»
отыскивается наибольшая степень достижения цели. В случае же
многоцелевой оптимизации, как уже отмечалось, степень дости-
жения абсолютного оптимума не может быть наибольшей по всем
критериям сразу, а, следовательно, возникает проблема ее измере-
ния. В абсолютном измерении степень достижения цели по пока-
зателю s может быть рассчитана по формуле (()) s s f x - f , т. е. как
степень удаления текущего значения функции от наименьшего ее
значения (от найденных субоптимальных планов). Графически это
выглядит следующим образом.
Поскольку компоненты целевой вектор-функции задаются в
различных единицах и масштабе, то для сопоставления различ-
ных степеней достижения цели при поиске компромиссного пла-
на их необходимо нормировать.
Нормирование степени достижения оптимума по критерию s
можно осуществить следующим образом:
() , 0 £ (x) £1 s
Введя функционал, формализующий понятие степени дости-
жения цели, приступим к формализации принятой схемы компро-
мисса, т. е., коль скоро невозможно достичь максимальной степе-
ни достижения цели по всем критериям сразу, зададимся целью,
чтобы наибольшей была минимальная по любому из критериев
степень достижения оптимума. Это означает, что если мы достиг-
ли максимума наихудшей степени достижения оптимума по како-
му-либо критерию, то по всем остальным критериям степень дос-
тижения цели будет не меньшей (равной или большей).
Многоцелевая модель, формализующая вышесказанное, долж-
на быть записана следующим образом:
max min s (x)
j ³ j "
() min (), .
Вводя новую переменную модели min s (x)
l = j , получим
Или в окончательном виде:
- D l ³ "
Полученная модель при линейности исходной модели явля-
ется также линейной с незначительным увеличением ее размер-
ности (на одну переменную и s дополнительных ограничений).
При решении многоцелевых задач у пользователя может поя-
виться желание отразить в модели неравнозначность (относитель-
ную важность) оптимизируемых целевых показателей. Сделать это
достаточно просто с помощью соответствующего вектора весовых
коэффициентов Î s
a . Модель в этом варианте будет иметь сле-
дующий вид:
- a D l ³ "
Однако при использовании данного подхода значительную
сложность представляет обоснование величин s
a . Надежного, на-
учно обоснованного метода их получения нет. Вся тяжесть реше-
ния этой задачи ложится на принимающего решение. При этом,
как показывают исследования, компромисс, основанный на ис-
пользовании весов s
a , очень неустойчив: «малым» изменениям от-
дельных величин могут соответствовать очень «большие» измене-
ния в результатах решения. Практически это ставит под сомнение
целесообразность «взвешивания» целевых показателей с целью
учесть в модели их относительную важность.
В то же время использование весовых коэффициентов s
весьма эффективно при практической реализации настоящей мо-
дели в режиме диалога. Действительно, при анализе текущего
компромиссного плана возможна, например, ситуация перевыпол-
нения установленных заданий по одной группе показателей и не-
довыполнения – по другой. В этом случае, последовательно
уменьшая в режиме диалога весовые коэффициенты по первой
группе показателей, целесообразно продолжить поиск рациональ-
ного решения, удовлетворяющего пользователя. Правда, при этом
необходимо помнить о высокой «неустойчивости» результатов от-
носительно весовых коэффициентов.
Контрольные вопросы.
1. Поясните понятие множество Парето.
2. В чем заключается алгоритм метода уступок?
3. Приведите примеры задач, при решении, которых необхо-
димо применять несколько критериев.
Метод главного критерия
Методы последовательной оптимизации
Недостатки свёртывания нескольких критериев заставляют искать другие подходы к решению задач многокритериального выбора. В данной лекции мы будем рассматривать методы последовательной оптимизации.
К методам последовательной оптимизации относят метод последовательных уступок и как частный случай данного метода – метод главного критерия , лексикографический критерий и метод равенства частных критериев .
Существует один, часто применяемый способ свести многокритериальную задачу к однокритериальной – это выделить один (главный, основной) критерий F 1 и стремиться его обратить в максимум (минимум), а на остальные F 2 , F 3 , . . Fm частные критерии наложить только некоторые ограничения, потребовав, чтобы они были не меньше (больше) каких-то заданных величин. Таким образом, идея метода главного критерия заключается в том, что частные критерии обычно неравнозначны между собой (одни из них более важны, чем другие) и это позволяет выделит главный критерий, а остальные (критерии) рассматривать как дополнительные, сопутствующие. Например, при оптимизации плана работы предприятия можно потребовать, чтобы прибыль была максимальна, план по ассортименту – выполнен или перевыполнен, а себестоимость продукции – не выше заданной. При таком подходе все показатели, кроме одного – главного, переводятся в разряд ограничений. Такое различие позволяет сформулировать задачу многокритериальной оптимизации как задачу нахождения условного экстремума основного (главного) критерия:
Встречаются случаи, когда пользователь готов на некоторое снижение величин более важных критериев, чтобы повысить величину менее важных. В таких ситуациях можно воспользоваться методом уступок . Идею этого метода можно изложить следующим образом.
Метод последовательных уступок. Согласно этому методу локальные критерии предварительно ранжируются по важности. Затем ищется наилучшее решение по наиболее важному критерию. На следующем шаге ищется решение наилучшее по следующему по важности критерию, причем допускается потеря в значении первого критерия не более чем на некоторую обусловленную величину, т.е. делается уступка по первому критерию. На третьем шаге оптимизируется решение по третьему критерию, при заданных уступках по первому и второму и т.д., пока не будет рассмотрен последний по важности критерий. При решении многокритериальных задач методом последовательных уступок вначале нужно определить важность частных критериев, т.е. расположить частные критерии в порядке убывания важности. Таким образом, главным считается критерий F 1 , менее важным F 2 , . . . , F m . Минимизируется первый по важности критерий и определяется его наименьшее значение F 1 min . Затем назначается величина допустимого снижения уступки D 1 ³0 критерия F 1 и ищется наименьшее значение критерия F 2 при условии, что значение F 1 должно быть не больше, чем F 1 min +D 1 . Снова назначается уступка D 2 ³0, но уже по второму критерию, которая вместе с первой используется при нахождении условного минимума F 3 и т.д. Наконец, минимизируется последний по важности критерий F m при условии, что значения каждого критерия F i из m-1 предыдущих должны быть не больше соответствующей величины F i min +D i .Получаемое в итоге решение считается оптимальным.Таким образом, оптимальным считается всякое решение, являющимся решением последней задачи из следующей последовательности задач
1) Найти F 1 min =min F 1 (X)
2) Найти F 2 min .=min F 2 (X) (1)
F 1 £ F 1 min +D 1
m) Найти F m min .=min F m (X)
F i £ F imin +D i
i=1,2, . . . ,m-1
Величины уступок выбирают в пределах инженерной точности, т.е. 5-10% от наименьшего значения критерия.
Пример. Пусть в области D={0;4} заданы два критерия F 1 (x)=(x-1) 2 +1 F 2 (x)=(x-2) 2 +2, которые нужно минимизировать (рис.1). Критерий F 1 важнее критерия F 2 (F 1 предпочтительнее F 2).
Рис.1. Графики функций F 1 и F 2
1. Согласно алгоритму минимизируем первый по важности критерий, и определяется его наименьшее значение F 1 min .Формулируем задачу оптимизации
найти min F 1 (x)= min[(x-1) 2 +1]
при ограничениях
Минимум для первого критерия достигается в точке x 1 opt =1 и равен F 1 (x 1 opt)=1
2. Затем назначается величина уступки D 1 =0.1 критерия F 1 и ищется наименьшее значение критерия F 2 при условии, что значение F 1 должно быть не больше, чем F 1 min +D 1 . Таким образом, мы получили следующую задачу оптимизации
minF 2 (x)=min[(x-2) 2 +2]
при ограничениях
(x-1) 2 +1£1+0.1
Для решения воспользуемся методом множителей Лагранжа. В результате получим безусловную задачу оптимизации
Ф(x, λ)= (x-2) 2 +2+ λ((x-1) 2 -0.1).
Находим частные производные и приравниваем их к нулю. В результате получим систему уравнений
Решая эту систему, получим x 2 opt =1.32.
Согласно алгоритму, решение, полученное на последнем этапе, и будет считаться оптимальным, т.е. x opt =1.32.
Решим данную задачу, используя систему MathCad.
f(x):=(x-2) 2 +2 целевая функция
x:=1 начальное приближение
| ограничения |
p:=Minimize(f,x) p=1.316.
Ответ: x opt =1.32.
Зам. Метод последовательных уступок целесообразно применять для решения тех инженерных задач, в которых все частные критерии упорядочены по степени важности, причём каждый критерий настолько более важен, чем последующий, что можно ограничиться учётом только попарной связи критериев и выбирать величину допустимого снижения очередного критерия с учётом поведения лишь одного следующего критерия.
Недостатком метода являются трудности с назначением и согласованием величин уступок, возрастающие с ростом размерности векторного критерия, а также необходимость формированиянеизменного для всей задачи априорного ранжирования критериев.
Как видим, в методе уступок предполагается, что разница в важности критериев не слишком велика. Можно предположить, что величина уступок как-то связана с нашим ощущением этой разницы.
Чтобы получить более полную характеристику достоинств и недостатков проектируемого объекта, нужно ввести больше критериев качества в рассмотрение. Как результат, задачи проектирования сложных систем всегда многокритериальные, так как при выборе наилучшего варианта приходится учитывать много различных требований, предъявленных к системе .
С привычной точки зрения задача со многими критериями решения не имеет, но к счастью это не так, всегда есть возможность одновременного удовлетворения всех заданных условий . А так, как практически любая подобная ситуация допускает разные компромиссные разрешения, то и подходы к их поиску многочисленны и весьма разнообразны.
Перечислим некоторые из подходов к решению задач многокритериальной оптимизации:
1. Метод уступок – лицо, принимающее решения подводится к выбору решения путем постепенного ослабления первоначальных требований, как правило, одновременно невыполнимых.
2. Метод идеальной точки – в области допустимых значений неизвестных ищется такая их совокупность, которая способна обеспечить набор значений критериев, в том или ином смысле ближайший к наилучшему варианту.
3. Метод свертывая – лицо, принимающее решения сводит многокритериальную задачу к задаче с одним критерием.
Ниже, рассмотрим подробно этих методов решения задачи многокритериальной оптимизации .
2.1. Метод последовательных уступок
Метод последовательных уступок решения многокритериальных задач применяется в случае, когда частные критерии могут быть упорядочены в порядке убывающей важности . Предположим, что все критерии максимизируются и пронумерованы в порядке убывания их важности. Вначале определяется максимальное значение , первого по важности критерия в области допустимых решений, решив задачу
Затем назначается, исходя из практических соображений и принятой точности, величина допустимого отклонения (экономически оправданной уступки) критерияи отыскивается максимальное значение второго критерияпри условии, что значение первого должно отклоняться от максимального не более чем на величину допустимой уступки, т.е. решается задача
![]()
Снова назначается величина уступки по второму критерию, которая вместе с первой используется при нахождении условного экстремума третьего частного критерия и т.д. Наконец, выявляется экстремальное значение последнего по важности критерияпри условии, что значение каждого из первыхчастных критериев отличается от экстремального не более чем на величину допустимой уступки. Получаемое на последнем этапе решение считается оптимальным.
Существенным недостатком метода последовательных уступок является то, что решение, полученное этим методом, может оказаться неоптимальным по Парето .
Рассмотрим пример, математическая модель трехкритериальной задачи имеет вид :


Уступка по первому критерию , а по второму.
Открываем электронную книгу Excel и, как и для решения однокритериальной задачи определяем ячейки под переменные . Для этого в ячейку А2 вводим подпись «Переменные», а соседние три ячейки В2, С2 и D2 вводим значения переменных. Это могут быть произвольные числа, например единицы или нули, далее они будут оптимизироваться.

рис. 2.1. Определение переменных значений
В третьей строке задаем целевые функции. В А3 вводим подпись «Целевые», а в В3 формулой «=2*B2+C2-3*D2» задаем первую целевую функцию . Аналогично в С3 и D3 вводим вторуюи третьюцелевую функцию, вводя в С3 «=B2+3*C2-2*D2», а в D3 «=-B2+2*C2+4*D2».

рис.2.2. Определение целевых значений
Ячейка А5 будем называть «Ограничения».

Левые части ограничений распишем от B5:D7, правые части записываем в диапазонF5:F7. Вводим в Е5 формулу «=B5*$B$2+C5*$C$2+D5*$D$2», номера столбцов и номера строк ряда переменных зафиксировано, далее воспользуемся автозаполнением, чтобы заполнить ячейки Е6 и Е7.

рис.2.3. Определение ограничений
Предварительные действия завершены. Вызываем надстройку «Поиск решения» в меню «Данные».
На первом этапе оптимизируем первую целевую функцию. После открытия окна «Поиск решения» в поле «Оптимизировать целевую функцию» ставим курсор и делаем ссылку на ячейку «В3», щелкая по ней мышью. В окне появится $B$3. В связи с тем, что целевая функция максимизируется, далее нужно проверить, что флажок ниже поля стоит напротив надписи «Максимум».
После ставим курсор в поле «Изменяя ячейки переменных» и обводим ячейки с переменными В2, С2 и D2, выделяя ячейки с переменными. В поле появиться $B$2:$D$2.
В нижней части окна находится поле «Ограничения». Для того, чтобы ввести ограничения, нажимаем кнопку «Добавить», откроется окно «Добавление ограничения». В левом поле «Ссылка на ячейки» вводят ссылку на левую часть первого ограничения – ячейку «Е5», в центральном окне определяем знак«»и в правом «Ограничения» выбираем соответствующую правую часть первого ограничения –«F5». Нажимаем «ОК», видим, что ограничение появилось в окне. Нажимаем вновь «Добавить», вводим «E6» «» и «F6». Вновь нажимаем «Добавить», вводим «E7» «≤» и «F7».
Для ввода дополнительных ограничений вновь нажимаем «Добавить», ставим курсор в левое поле и обводим ячейки В2, С2 и D2 (результат $B$2:$D$2) в среднем окне ставим «» и в правом число 0.

рис. 2.4. Параметры поиска решения

рис.2.5. Результат полученного решения
На втором этапе оптимизируется вторая целевая функция. Однако, первую, в соответствие с методом последовательных уступок, можно ухудшить первый критерий на величину не более, чем . По этой причине, на втором шаге, значения в ячейке В3 (где хранится первая целевая функция, которая максимизируется) может быть значение, не меньшее, чем 24,8 (=28,8-4). Для удобства, можно записать «Уступок» в сторонке.
Вызываем надстройку «Поиск решения», видно, что все прежние данные остались введенными. Меняем ссылку на целевую функцию. Ставим курсор в поле «Оптимизировать целевую функцию» и щелкаем по ячейке С3, в которой находится ссылка на вторую целевую функцию. Так, как вторая целевая минимизируется, то ставим флажок в поле напротив надписи «Минимум». Вводим дополнительное ограничение, связанное с уступкой по первому критерию. Переводим курсор в поле «Ограничения» и нажимаем кнопку «Добавить», правее поля. В появившемся окне «Добавление ограничения» в трех окнах (слева на право) вводим данные «В3», «≥», «С9».
Результат – переменные равны 10,2; 4,4; 0. Вторая целевая функция равна 23,4 (ячейка С3). Первая равна своему минимальному значению 24,8 (ячейка В3).

рис.2.6. Определение уступка
На третьем этапе делаем уступку по второму критерию. Величина уступки равна . Так, как вторая функция минимизируется, то ее значение не должно превышать 23,4+5=28,4. Вызываем надстройку «Поиск решения». Меняем ссылку на целевую функцию. Ставим курсор в поле «Оптимизировать целевую функцию» и щелкаем по ячейке D3, в которой находится ссылка на третью целевую функцию. Так, как третья целевая максимизируется, то ставим флажок в поле напротив надписи «Максимум». Вводим дополнительное ограничение, связанное с уступкой по второму критерию. Переводим курсор в поле «Ограничения» и нажимаем кнопку «Добавить». В появившемся окне «Добавление ограничения», вводим данные «С3», «≤», «С10».
Результат – переменные равны 10,76; 6,62; 1,11. Целевые функции равны, соответственно, 24,8; 28,4 и 6,93. Это окончательный ответ. Все дополнительные условия соблюдены.

рис.2.7. Окончательный результат решения по методу последовательного уступка
Метод последовательных уступок.
Рассмотрим один из методов, использующих ограничения на критерии – метод последовательных уступок . Алгоритм метода следующий:
1. Критерии нумеруются в порядке убывания важности.
2. Решается задача
![]() ;
;
Определяется значение .
3. Устанавливается уступка , по этому критерию.
4. Решается задача
 ;
;
Если в задаче более двух критериев, то пункты 3 и 4 повторяются для ,..., .
Субоптимальный план, найденный при решении последней задачи, является оптимальным компромиссным планом в данной схеме компромисса.
Метод последовательных уступок, являясь простым и понятным в реализации, обладает, тем не менее, целым рядом недостатков, основными из которых являются:
1. Сложность и субъективизм в ранжировании критериев.
2. Субъективизм в задании величин уступок.
3. Степени достижения оптимума (безусловного) по всем критериям, кроме первого, не определены. Рассчитать их можно, лишь решив исходные модели по соответствующим целевым функциям (еще (k - 1) задач) на глобальный оптимум.
4. Поскольку уступка по последнему критерию не делается, степень достижения оптимума по нему может оказаться совершенно неудовлетворительной. Для «исправления» плана в этом случае вес расчеты должны быть повторены с другими (причем не гарантирующими нужных окончательных результатов) коэффициентами уступок.
Пример. Решить задачу методом последовательных уступок, если уступка по первому критерию составляет 10% от его оптимального значения.

Решим задачу по критерию . Получим . В соответствии с условием задачи величина уступки . Дополнительное ограничение будет иметь вид ![]() , то есть
, то есть ![]() . Решая задачу
. Решая задачу

получим , ,
Задача 1.
Предприятие может выпускать пять видов продукции И1, И2, ИЗ, И4, И5. Для этого используется три вида ресурсов, расход которых на производство единицы продукции и их запасы приведены в таблице:
| Ресурс | И1 | И2 | ИЗ | И4 | И5 | Запасы |
| В 1 | ||||||
| В 2 | ||||||
| В 3 |
Все изделия обрабатываются на станках четырех типов. Норма времени на обработку одного изделия и фонд времени работы станков приведены в таблице:
Объем каждого вида продукции должен быть не менее 100 и не более 500 единиц. Мерой эффективности производственной программы являются следующие показатели:
1. Прибыль предприятия – f 1 ;
2. Валовый объем выпуска продукции в стоимостном выражении – f 2 ;
3. Себестоимость продукции – f 3 ;
4. Уровень загрузки оборудования – f 4 .
Требуется.
1. Решить задачу методом последовательных уступок, если уступку по каждому критерию полагать равной 10% от его оптимального значения.
2. Решить задачу методом свертывания критериев, выбрав вектор весовых коэффициентов методом парных сравнений.
Решение.
1. Составим ЭММ задачи.
Обозначим через – количество продукции И1, – количество продукции И2, – количество продукции И3, – количество продукции И4, – количество продукции И5.
Целевые функции будут иметь вид:
Прибыль: .
Валовый объем (в стоимостном выражении).
Встречаются случаи, когда пользователь готов на некоторое снижение величин более важных критериев, чтобы повысить величину менее важных. В таких ситуациях можно воспользоваться методом уступок . Идею этого метода можно изложить следующим образом.
Метод последовательных уступок. Согласно этому методу локальные критерии предварительно ранжируются по важности. Затем ищется наилучшее решение по наиболее важному критерию. На следующем шаге ищется решение наилучшее по следующему по важности критерию, причем допускается потеря в значении первого критерия не более чем на некоторую обусловленную величину, т.е. делается уступка по первому критерию. На третьем шаге оптимизируется решение по третьему критерию, при заданных уступках по первому и второму и т.д., пока не будет рассмотрен последний по важности критерий. При решении многокритериальных задач методом последовательных уступок вначале нужно определить важность частных критериев, т.е. расположить частные критерии в порядке убывания важности. Таким образом, главным считается критерий F 1 , менее важным F 2 , . . . , F m . Минимизируется первый по важности критерий и определяется его наименьшее значение F 1 min . Затем назначается величина допустимого снижения уступки D 1 ³0 критерия F 1 и ищется наименьшее значение критерия F 2 при условии, что значение F 1 должно быть не больше, чем F 1 min +D 1 . Снова назначается уступка D 2 ³0, но уже по второму критерию, которая вместе с первой используется при нахождении условного минимума F 3 и т.д. Наконец, минимизируется последний по важности критерий F m при условии, что значения каждого критерия F i из m-1 предыдущих должны быть не больше соответствующей величины F i min +D i .Получаемое в итоге решение считается оптимальным.Таким образом, оптимальным считается всякое решение, являющимся решением последней задачи из следующей последовательности задач
1) Найти F 1 min =min F 1 (X)
2) Найти F 2 min .=min F 2 (X) (1)
F 1 £ F 1 min +D 1
m) Найти F m min .=min F m (X)
F i £ F imin +D i
i=1,2, . . . ,m-1
Величины уступок выбирают в пределах инженерной точности, т.е. 5-10% от наименьшего значения критерия.
Пример. Пусть в области D={0;4} заданы два критерия F 1 (x)=(x-1) 2 +1 F 2 (x)=(x-2) 2 +2, которые нужно минимизировать (рис.1). Критерий F 1 важнее критерия F 2 (F 1 предпочтительнее F 2).
Рис.1. Графики функций F 1 и F 2
1. Согласно алгоритму минимизируем первый по важности критерий, и определяется его наименьшее значение F 1 min .Формулируем задачу оптимизации
найти min F 1 (x)= min[(x-1) 2 +1]
при ограничениях
Минимум для первого критерия достигается в точке x 1 opt =1 и равен F 1 (x 1 opt)=1
2. Затем назначается величина уступки D 1 =0.1 критерия F 1 и ищется наименьшее значение критерия F 2 при условии, что значение F 1 должно быть не больше, чем F 1 min +D 1 . Таким образом, мы получили следующую задачу оптимизации
minF 2 (x)=min[(x-2) 2 +2]
при ограничениях
(x-1) 2 +1£1+0.1
Для решения воспользуемся методом множителей Лагранжа. В результате получим безусловную задачу оптимизации
Ф(x, λ)= (x-2) 2 +2+ λ((x-1) 2 -0.1).
Находим частные производные и приравниваем их к нулю. В результате получим систему уравнений

Решая эту систему, получим x 2 opt =1.32.
Согласно алгоритму, решение, полученное на последнем этапе, и будет считаться оптимальным, т.е. x opt =1.32.
Решим данную задачу, используя систему MathCad.
f(x):=(x-2) 2 +2 целевая функция
x:=1 начальное приближение