Соотношение (в математике) - это взаимосвязь между двумя или более числами одного рода. Соотношения сравнивают абсолютные величины или части целого. Соотношения вычисляются и записываются по-разному, но основные принципы одинаковы для всех соотношений.
Шаги
Часть 1
Определение соотношений-
Определение соотношений. Соотношение - это взаимосвязь между двумя (или более) значениями одного рода. Например, если для приготовления торта необходимы 2 стакана муки и 1 стакан сахара, то соотношение муки к сахару равно 2 к 1.
- Соотношения могут быть использованы и в тех случаях, когда две величины не связаны друг с другом (как в примере с тортом). Например, если в классе учатся 5 девочек и 10 мальчиков, то соотношение девочек к мальчикам равно 5 к 10. Эти величины (число мальчиков и число девочек) не зависят друг от друга, то есть их значения изменятся, если кто-то уйдет из класса или в класс придет новый ученик. Соотношения просто сравнивают значения величин.
-
Обратите внимание на разные способы представления соотношений. Соотношения могут быть представлены словами или при помощи математических символов.
- Очень часто соотношения выражены словами (как показано выше). Особенно такая форма представления соотношений применяется в повседневной жизни, далекой от науки.
- Также соотношения можно выразить через двоеточие. При сравнении двух чисел в соотношении вы будете использовать одно двоеточие (например, 7:13); при сравнении трех и более значений ставьте двоеточие между каждой парой чисел (например, 10:2:23). В нашем примере с классом вы можете выразить соотношение девочек и мальчиков так: 5 девочек: 10 мальчиков. Или так: 5:10.
- Реже соотношения выражаются при помощи наклонной черты. В примере с классом оно может быть записано так: 5/10. Тем не менее это не дробь и читается такое соотношение не как дробь; более того, запомните, что в соотношении цифры не представляют собой часть единого целого.
Часть 2
Использование соотношений-
Упростите соотношение. Соотношение можно упростить (аналогично дробям), разделив каждый член (число) соотношения на . Однако при этом не упустите из виду исходных значений соотношения.
- В нашем примере в классе 5 девочек и 10 мальчиков; соотношение равно 5:10. Наибольший общий делитель членов соотношения равен 5 (так как и 5, и 10 делятся на 5). Разделите каждое число соотношения на 5 и получите соотношение 1 девочка к 2 мальчикам (или 1:2). Однако при упрощении соотношения помните об исходных значениях. В нашем примере в классе не 3 ученика, а 15. Упрощенное соотношение сравнивает количество мальчиков и количество девочек. То есть на каждую девочку приходится 2 мальчика, но в классе не 2 мальчика и 1 девочка.
- Некоторые соотношения не упрощаются. Например, соотношение 3:56 не упрощается, так как у этих чисел нет общих делителей (3 - простое число, а 56 не делится на 3).
-
Используйте умножение или деление для увеличения или уменьшения соотношения. Распространены задачи, в которых необходимо увеличить или уменьшить два значения, пропорциональных друг другу. Если вам дано соотношение и нужно найти соответствующее ему большее или меньшее соотношение, умножьте или разделите исходное соотношение на некоторое данное число.
- Например, пекарю нужно утроить количество ингредиентов, данных в рецепте. Если по рецепту соотношение муки к сахару составляет 2 к 1 (2:1), то пекарь умножит каждый член соотношения на 3 и получит соотношение 6:3 (6 чашек муки к 3 чашкам сахара).
- С другой стороны, если пекарю необходимо уполовинить количество ингредиентов, данных в рецепте, то пекарь разделит каждый член соотношения на 2 и получит соотношение 1:½ (1 чашка муки к 1/2 чашке сахара).
-
Поиск неизвестного значения, когда даны два эквивалентных соотношения. Это задача, в которой необходимо найти неизвестную переменную в одном соотношении при помощи второго соотношения, которое эквивалентно первому. Для решения таких задач пользуйтесь . Запишите каждое соотношение в виде обыкновенной дроби, поставьте между ними знак равенства и перемножьте их члены крест-накрест.
- Например, дана группа учеников, в которой 2 мальчика и 5 девочек. Каково будет число мальчиков, если число девочек увеличить до 20 (пропорция сохраняется)? Во-первых, запишите два соотношения - 2 мальчика:5 девочек и х мальчиков:20 девочек. Теперь запишите эти соотношения в виде дробей: 2/5 и х/20. Перемножьте члены дробей крест-накрест и получите 5x = 40; следовательно, х = 40/5 = 8.
Часть 3
Распространенные ошибки-
Избегайте сложения и вычитания в текстовых задачах на соотношение. Многие текстовые задачи выглядят примерно так: «В рецепте необходимо использовать 4 клубня картофеля и 5 корнеплодов моркови. Если вы хотите добавить 8 клубней картофеля, то сколько понадобится моркови, чтобы соотношение осталось неизменным?» При решении подобных задач ученики часто допускают ошибку, прибавляя одинаковое количество ингредиентов к исходному числу. Однако, чтобы сохранить соотношение, нужно использовать умножение. Вот примеры правильного и неправильного решения:
- Неверно: «8 - 4 = 4 - так мы добавили 4 клубня картофеля. Значит, нужно взять 5 корнеплодов моркови и к ним добавить еще 4... Стоп! Соотношения так не вычисляют. Стоит попробовать снова».
- Верно: «8 ÷ 4 = 2 - значит, мы умножили количество картофеля на 2. Соответственно, 5 корнеплодов моркови тоже нужно умножить на 2. 5 x 2 = 10 - в рецепт нужно добавить 10 корнеплодов моркови». В текстовых задачах гораздо проще распознать ошибку, если записывать единицы измерения после каждого значения. Помните, что величины с одними и теми же единицами измерения в числителе и знаменателе сокращаются. Сократив выражение, вы получите верный ответ.
- Пример: дано 6 коробок, в каждой третьей коробке находится 9 шариков. Сколько всего шариков?
- Неверно: 6 коробок x 3 коробки/9 шариков = ... Стоп, ничего нельзя сократить. Ответ будет таким: «коробки x коробки / шарики». Он не имеет смысла.
- Верно: 6 коробок x 9 шариков/3 коробки = 6 коробок * 3 шарика/1 коробку = 6 коробок * 3 шарика/1 коробку = 6 * 3 шарика/1 = 18 шариков.
Использование соотношений. Соотношения используются как в науке, так и в повседневной жизни для сравнения величин. Простейшие соотношения связывают только два числа, но есть соотношения, сравнивающие три или более значения. В любой ситуации, в которой присутствует более одной величины, можно записать соотношение. Связывая некоторые значения, соотношения могут, например, подсказать, как увеличить количество ингредиентов в рецепте или веществ в химической реакции.
Относительные величины бывают четырех видов: интенсивные, экстенсивные, показатели соотношения, показатели наглядности.
Интенсивные показатели - показывают частоту явления в среде. В качестве среды обычно выступает некая совокупность объектов (населения, пациентов, случаев), у части которых происходит какое-то явление. Рассчитывается по следующей формуле:
И.п. = явление/среда*коэффициент.
Коэффициент используется для удобства представления показателя, представляет собой различные степени числа 10 и обычно принимает значения 100, 1000, 10 000, 100 000. Его величина зависит от частоты встречаемости явления: чем реже встречается, тем больше коэффициент. Так, показатели рождаемости, смертности, общей заболеваемости населения обычно рассчитываются на 1000 человек. При расчете материнской смертности, как значительно более редкого события, используется коэффициент 100 000. Наоборот, частота такого распространенного явления, как случай временной утраты трудоспособности, рассчитывается на 100 работающих.
Пример расчета интенсивного показателя:
За год в больнице Н. было выполнено 360 хирургических операций. В 54 случаях в послеоперационном периоде наблюдались различные осложнения. Найти частоту послеоперационных осложнений из расчета на 100 операций.
Решение: Частота послеоперационных осложнений - это интенсивный показатель, который может быть рассчитан как отношение явления к среде. Средой выступает совокупность выполненных операций (360), из числа которых в 54 случаях, как следует из условия задачи, происходило явление - отмечались послеоперационные осложнения. Таким образом:
Частота послеоперационных осложнений = (Число случаев послеоперационных осложнений) / (Число выполненных операций) * 100 = (54 / 360) * 100 = 15.
Значение коэффициента принято равным 100, так как в условии задачи спрашивается частота, рассчитанная на 100 выполненных операций.
Ответ: Частота послеоперационных осложнений в больнице Н. за год составила 15 случаев на 100 выполненных операций.
Экстенсивные показатели - характеризуют структуру явления, измеряются в процентах, реже - в промилле или долях единицы. Экстенсивные величины показывают, какую часть составляет отдельная группа единиц в структуре всей совокупности. Рассчитываются по формуле:
Э.п. = часть/целое*100%.
Пример расчета экстенсивного показателя:
В исследовании эффективности лечения пневмонии с использованием нового антибиотика приняли участие 200 пациентов, из них 90 - мужчины. Необходимо определить долю мужчин среди исследуемых, результат выразить в %.
Решение: Пациенты мужского пола представляют собой часть от всей совокупности исследуемых. Следовательно, мы должны воспользоваться формулой для расчета экстенсивных показателей:
Доля пациентов мужского пола среди всех исследуемых = (число мужчин) / (число всех пациентов) * 100% = (90 / 200) * 100% = 45%.
Ответ: Доля пациентов в структуре исследуемых составляет 45%.
Показатели соотношения - характеризуют отношение двух не связанных между собой совокупностей. Данные совокупности могут измеряться в одних величинах, главное условие, что их изменения должны происходить независимо друг от друга. Обычно в таком виде представляются различные индексы, коэффициенты, показатели обеспеченности населения. Рассчитываются по следующей формуле:
П.с. = (первая совокупность) / (вторая совокупность)*коэффициент
Коэффициент обычно принимает значения 1 (для индексов) или 10 000 (для показателей обеспеченности населения).
Пример расчета показателя соотношения:
В одном из районов Республики Татарстан проживает 40 000 населения. В лечебно-профилактических учреждениях данного района развернуты 384 стационарные койки. Какова обеспеченность населения койками в районе?
Решение: Мы имеем две совокупности: население и стационарные койки. Изменения числа населения не зависят от изменений числа стационарных коек и наоборот, в связи с чем делаем вывод о том, что представленные совокупности не связаны между собой. Рассчитаем показатель обеспеченности населения стационарными койками:
Обеспеченность населения койками = (число коек) / (численность населения) *10 000 = (384 / 40 000) * 10 000 = 96.
Ответ: Обеспеченность населения стационарными койками составляет 96 на 10 000 населения.
Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.
Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.
Линейное уравнение
Уравнения вида ax+by=c называют линейными. Обозначения x, y - это неизвестные, значение которых надо найти, b, a - коэффициенты при переменных, c - свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.
Виды систем линейных уравнений
Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 - функции, а (x, y) - переменные функций.
Решить систему уравнений - это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или решения не существует их называют равносильными.
Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака "равенство" часть имеет значение или выражена функцией, такая система неоднородна.
Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.
Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.
Основная задача при обучении способам решения - это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем решение примера системы линейных уравнений 7 класса методом подстановки:

Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:

Решение с помощью алгебраического сложения
При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.

Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
- Почленно сложить полученное выражение и найти одно из неизвестных.
- Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.
Способ решения введением новой переменной
Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.
Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.

Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 - 4*a*c, где D - искомый дискриминант, b, a, c - множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Решение для полученных в итоге системы находят методом сложения.
Наглядный метод решения систем
Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.

Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.

Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.

Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n - строк и m - столбцов.
Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей - вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Обратная матрица - это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение - одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.
Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y - только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 - обратная матрица, а |K| - определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.
Определитель легко вычисляется для матрицы "два на два", необходимо лишь помножить друг на друга элементы по диагонали. Для варианта "три на три" существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Решение примеров систем линейных уравнений матричным методом
Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.

В примере a nm - коэффициенты уравнений, матрица - вектор x n - переменные, а b n - свободные члены.


Решение систем методом Гаусса
В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса - Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 - соответственно с 3-мя и 4-мя переменными.
После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:

Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .

Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.
Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.
Для простоты записи вычислений принято делать следующим образом:

Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака "стрелка" и продолжают выполнять необходимые алгебраические действия до достижения результата.
В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
Достаточно часто при анализе экономических систем приходится решать так называемые задачи массового обслуживания, возникающие в следующей ситуации. Пусть анализируется система технического обслуживания автомобилей, состоящая из некоторого количества станций различной мощности. На каждой из станций (элемента системы) могут возникать, по крайней мере, две типичные ситуации:
- число заявок слишком велико для данной станции, возникают очереди, и за задержки в обслуживании приходится платить;
- на станцию поступает слишком мало заявок и теперь уже приходится учитывать потери, вызванные простоем станции.
Ясно, что цель системного анализа в данном случае заключается в определении некоторого соотношения между потерями доходов по причине очередей и потерями по причине простоя станций.
Теория массового обслуживания – специальный раздел теории систем – это раздел теории вероятности, в котором изучаются системы массового обслуживания с помощью математических моделей.
Система массового обслуживания (СМО) – это модель, включающая в себя: 1) случайный поток требований, вызовов или клиентов, нуждающихся в обслуживании; 2) алгоритм осуществления этого обслуживания; 3) каналы (приборы) для обслуживания.
Примерами СМО являются кассы, АЗС, аэропорты, продавцы, парикмахеры, врачи, телефонные станции и другие объекты, в которых осуществляется обслуживание тех или иных заявок.
Задача теории массового обслуживания состоит в выработке рекомендаций по рациональному построению СМО и рациональной организации их работы с целью обеспечения высокой эффективности обслуживания при оптимальных затратах.
Главная особенность задач данного класса – явная зависимость результатов анализ и получаемых рекомендаций от двух внешних факторов: частоты поступления и сложности заказов (а значит и времени их исполнения).
Предмет теории массового обслуживания – это установление зависимости между характером потока заявок, производительностью отдельного канала обслуживания, числом каналов и эффективностью обслуживания.
В качестве характеристик СМО рассматриваются:
- средний процент заявок, получающих отказ и покидающих систему не обслуженными;
- среднее время «простоя» отдельных каналов и системы в целом;
- среднее время ожидания в очереди;
- вероятность того, что поступившая заявка будет немедленно обслужена;
- закон распределения длины очереди и другие.
Добавим, что заявки (требования) поступают в СМО случайным образом (в случайные моменты времени), с точками сгущения и разрежения. Время обслуживания каждого требования также является случайным, после чего канал обслуживания освобождается и готов к выполнению следующего требования. Каждая СМО, в зависимости от числа каналов и их производительности, обладает некоторой пропускной способностью. Пропускная способность СМО может быть абсолютной (среднее число заявок, обслуживаемых в единицу времени) и относительной (среднее отношение числа обслуженных заявок к числу поданных).
3.1 Модели систем массового обслуживания.
Каждую СМО может характеризовать выражением: (a / b / c) : (d / e / f) , где
a - распределение входного потока заявок;
b - распределение выходного потока заявок;
c – конфигурация обслуживающего механизма;
d – дисциплина очереди;
e – блок ожидания;
f – емкость источника.
Теперь рассмотрим подробнее каждую характеристику.
Входной поток заявок – количество поступивших в систему заявок. Характеризуется интенсивностью входного потока l .
Выходной поток заявок – количество обслуженных системой заявок. Характеризуется интенсивностью выходного потока m .
Конфигурация системы подразумевает общее число каналов и узлов обслуживания. СМО может содержать:
- один канал обслуживания (одна взлетно-посадочная полоса, один продавец);
- один канал обслуживания, включающий несколько последовательных узлов (столовая, поликлиника, конвейер);
- несколько однотипных каналов обслуживания, соединенных параллельно (АЗС, справочная служба, вокзал).
Таким образом, можно выделить одно- и многоканальные СМО.
С другой стороны, если все каналы обслуживания в СМО заняты, то подошедшая заявка может остаться в очереди, а может покинуть систему (например, сбербанк и телефонная станция). В этом случае мы говорим о системах с очередью (ожиданием) и о системах с отказами.
Очередь – это совокупность заявок, поступивших в систему для обслуживания и ожидающих обслуживания. Очередь характеризуется длиной очереди и ее дисциплиной.
Дисциплина очереди – это правило обслуживания заявок из очереди. К основным типам очереди можно отнести следующие:
- ПЕРППО (первым пришел – первым обслуживаешься) – наиболее распространенный тип;
- ПОСППО (последним пришел – первым обслуживаешься);
- СОЗ (случайный отбор заявок) – из банка данных.
- ПР – обслуживание с приоритетом.
Длина очереди может быть
- неограничена – тогда говорят о системе с чистым ожиданием;
- равна нулю – тогда говорят о системе с отказами;
- ограничена по длине (система смешанного типа).
Блок ожидания – «вместимость» системы – общее число заявок, находящихся в системе (в очереди и на обслуживании). Таким образом, е=с+ d .
Емкость источника , генерирующего заявки на обслуживание – это максимальное число заявок, которые могут поступить в СМО. Например, в аэропорту емкость источника ограничена количеством всех существующих самолетов, а емкость источника телефонной станции равна количеству жителей Земли, т.е. ее можно считать неограниченной.
Количество моделей СМО соответствует числу всевозможных сочетаний этих компонент.
3.2 Входной поток требований.
С каждым отрезком времени [a , a + T ], свяжем случайную величину Х , равную числу требований, поступивших в систему за время Т .
Поток требований называется стационарным , если закон распределения не зависит от начальной точки промежутка а , а зависит только от длины данного промежутка Т . Например, поток заявок на телефонную станцию в течение суток (Т =24 часа) нельзя считать стационарным, а вот с 13 до 14 часов (Т =60 минут) – можно.
Поток называется без последействия , если предыстория потока не влияет на поступления требований в будущем, т.е. требования не зависят друг от друга.
Поток называется ординарным , если за очень короткий промежуток времени в систему может поступить не более одного требования. Например, поток в парикмахерскую – ординарный, а в ЗАГС – нет. Но, если в качестве случайной величины Х рассматривать пары заявок, поступающих в ЗАГС, то такой поток будет ординарным (т.е. иногда неординарный поток можно свести к ординарному).
Поток называется простейшим , если он стационарный, без последействия и ординарный.
Основная теорема. Если поток – простейший, то с.в. Х [ a . a + T ] распределена по закону Пуассона, т.е. .
Следствие 1 . Простейший поток также называется пуассоновским.
Следствие 2 . M (X )= M (Х [ a , a + T ] )= l T , т.е. за время Т l T заявок. Следовательно, за одну единицу времени в систему поступает в среднем l заявок. Эта величина и называется интенсивностью входного потока.
Рассмотрим ПРИМЕР.
В ателье поступает в среднем 3 заявки в день. Считая поток простейшим, найти вероятность того, что в течение двух ближайших дней число заявок будет не менее 5.
Решение.
По условию задачи, l
=3, Т
=2 дня, входной поток пуассоновский, n
³5. при решении удобно ввести противоположное событие, состоящее в том, что за время Т
поступит меньше 5 заявок. Следовательно, по формуле Пуассона, получим 
^
3.3 Состояние системы. Матрица и граф переходов.
В случайный момент времени СМО переходит из одного состояния в другое: меняется число занятых каналов, число заявок и очереди и пр. Таким образом, СМО с n каналами и длиной очереди, равной m , может находиться в одном из следующих состояний:
Е 0 – все каналы свободны;
Е 1 – занят один канал;
Е n – заняты все каналы;
Е n +1 – заняты все каналы и одна заявка в очереди;
Е n + m – заняты все каналы и все места в очереди.
Аналогичная система с отказами может находиться в состояниях E 0 – E n .
Для СМО с чистым ожиданием существует бесконечное множество состояний. Таким образом, состояниеE n СМО в момент времени t – это количество n заявок (требований), находящихся в системе в данный момент времени, т.е. n = n (t ) – случайная величина, E n (t ) – исходы этой случайной величины, а P n (t ) – вероятность пребывания системы в состоянии E n .
С состоянием системы мы уже знакомы. Отметим, что не все состояния системы равнозначны. Состояние системы называется источником , если система может выйти из этого состояния, но не может в него вернуться. Состояние системы называется изолированным, если система не может выйти из этого состояния или в него войти.
Для наглядности изображения состояний системы используют схемы (так называемые графы переходов), в которых стрелки указывают возможные переходы системы из одного состояния в другое, а также вероятности таких переходов.

Рисунок 3.1 – граф переходов
| Сост. | Е 0 | Е 1 | Е 2 | |
| Е 0 | Р 0,0 | Р 0,1 | Р 0,2 | |
| Е 1 | Р 1,0 | Р 1,1 | Р 1,2 | |
| Е 2 | Р 2,0 | Р 2,2 | Р 2,2 |
Также иногда удобно воспользоваться матрицей переходов. При этом первый столбец означает исходные состояния системы (текущие), а далее приведены вероятности перехода из этих состояний в другие.
Так как система обязательно перейдет из одного
состояния в другое, то сумма вероятностей в каждой строке всегда равна единице.
3.4 Одноканальные СМО.
3.4.1 Одноканальные СМО с отказами.
Будем рассматривать системы, удовлетворяющие требованиям:
(Р/Е/1):(–/1/¥) . Предположим также, что время обслуживания требования не зависит от количества требований, поступивших в систему. Здесь и далее «Р» означает, что входной поток распределен по закону Пуассона, т.е. простейший, «Е» означает, что выходной поток распределен по экспоненциальному закону. Также здесь и далее основные формулы даются без доказательства.
Для такой системы возможно два состояния: Е 0 – система свободна и Е 1 – система занята. Составим матрицу переходов. Возьмем D t – бесконечно малый промежуток времени. Пусть событие А состоит в том, что в систему за время D t поступило одно требование. Событие В состоит в том, что за время D t обслужено одно требование. Событие А i , k – за время D t система перейдет из состояния E i в состояние E k . Так как l – интенсивность входного потока, то за время D t в систему в среднем поступает l*D t требований. То есть, вероятность поступления одного требования Р(А)= l* D t , а вероятность противоположного событияР(Ā)=1- l*D t . Р(В)= F (D t )= P (b < D t )=1- e - m D t = m D t – вероятность обслуживания заявки за время D t . Тогда А 00 – заявка не поступит или поступит, но будет обслужена. А 00 =Ā+А* В. Р 00 =1- l*D t . (мы учли, что(D t ) 2 – бесконечно малая величина)
А 01 – заявка поступит, но не будет обслужена. А 01 =А*
 . Р 01 =
l*D
t
.
. Р 01 =
l*D
t
.
А 10 – заявка будет обслужена и новой не будет. А 10 =В* Ā. Р 10 = m*D t .
А 11 – заявка не будет обслужена или поступит новая, которая еще не обслужена. А 11 = +В*
А. Р 01 =1-
m*D
t
.
+В*
А. Р 01 =1-
m*D
t
.
Таким образом, получим матрицу переходов:
| Сост. | Е 0 | Е 1 |
| Е 0 | 1-l* Dt | l* Dt |
| Е 1 | m* Dt | 1-m* Dt |
Вероятность простоя и отказа системы.
Найдем теперь вероятность нахождения системы в состоянии Е
0
в любой момент времени t
(т.е. р
0
(
t
)
). График функции  изображен на рисунке 3.2.
изображен на рисунке 3.2.
Асимптотой графика является прямая  .
.
Очевидно, начиная с некоторого момента t
, 

1
Рисунок 3.2
Окончательно получим, что  и
и  , где р
1
(t
)
– вероятность того, что в момент времени t
система занята (т.е. находится в состоянии Е
1
).
, где р
1
(t
)
– вероятность того, что в момент времени t
система занята (т.е. находится в состоянии Е
1
).
Очевидно, что в начале работы СМО протекающий процесс не будет стационарным: это будет «переходный», нестационарный режим. Спустя некоторое время (которое зависит от интенсивностей входного и выходного потока) этот процесс затухнет и система перейдет в стационарный, установившийся режим работы, и вероятностные характеристики уже не будут зависеть от времени.
Стационарный режим работы и коэффициент загрузки системы.
Если вероятность нахождения системы в состоянии Е
k
, т.е. Р
k
(t
),
не зависит от времени t
, то говорят, что в СМО установился стационарный режим
работы. При этом величина  называется коэффициентом загрузки системы
(или приведенной плотностью потока заявок). Тогда для вероятностейр
0
(t
)
ир
1
(t
)
получаем следующие формулы:
называется коэффициентом загрузки системы
(или приведенной плотностью потока заявок). Тогда для вероятностейр
0
(t
)
ир
1
(t
)
получаем следующие формулы:  ,
,  . Можно также сделать вывод:чем больше коэффициент загрузки системы, тем больше вероятность отказа системы (т.е. вероятность того, что система занята).
. Можно также сделать вывод:чем больше коэффициент загрузки системы, тем больше вероятность отказа системы (т.е. вероятность того, что система занята).
На автомойке один блок для обслуживания. Автомобили прибывают по пуассоновскому распределению с интенсивностью 5 авто/час. Среднее время обслуживания одной машины – 10 минут. Найти вероятность того, что подъехавший автомобиль найдет систему занятой, если СМО работает в стационарном режиме.
Решение.
По условию задачи, l
=5, m
y
=5/6. Надо найти вероятность р
1
– вероятность отказа системы.  .
.
3.4.2 Одноканальные СМО с неограниченной длиной очереди.
Будем рассматривать системы, удовлетворяющие требованиям: (Р/Е/1):(d/¥/¥). Система может находиться в одном из состояний E 0 , …, E k , … Анализ показывает, что через некоторое время такая система начинает работать в стационарном режиме, если интенсивность выходного потока превышает интенсивность входного потока (т.е. коэффициент загрузки системы меньше единицы). Учитывая это условие, получим систему уравнений

решая которую найдем, что . Таким образом, при условии, что y
<1, получим  Окончательно,
Окончательно,  и
и  – вероятность нахождения СМО в состоянии Е
k
в случайный момент времени.
– вероятность нахождения СМО в состоянии Е
k
в случайный момент времени.
Средние характеристики системы.
За счет неравномерного поступления требований в систему и колебания времени обслуживания, в системе образуется очередь. Для такой системы можно исследовать:
- n – количество требований, находящихся в СМО (в очереди и на обслуживании);
- v – длину очереди;
- w – время ожидания начала обслуживания;
- w 0 – общее время нахождения в системе.
Нас будут интересовать средние характеристики (т.е. берем математическое ожидание от рассматриваемых случайных величин, и помним, что y <1).
 – среднее число заявок в системе.
– среднее число заявок в системе.
 – средняя длина очереди.
– средняя длина очереди.
 – среднее время ожидания начала обслуживания, т.е. время ожидания в очереди.
– среднее время ожидания начала обслуживания, т.е. время ожидания в очереди.
 – среднее время, которое заявка проводит в системе – в очереди и на обслуживании.
– среднее время, которое заявка проводит в системе – в очереди и на обслуживании.
На автомойке один блок для обслуживания и есть место для очереди. Автомобили прибывают по пуассоновскому распределению с интенсивностью 5 авто/час. Среднее время обслуживания одной машины – 10 минут. Найти все средние характеристики СМО.
Решение.
l
=5, m
=60мин/10мин = 6. Коэффициент загрузки y
=5/6. Тогда среднее число автомобилей в системе  , средняя длина очереди
, средняя длина очереди  , среднее время ожидания начала обслуживания
, среднее время ожидания начала обслуживания  часа = 50 мин, и, наконец, среднее время нахождения в системе
часа = 50 мин, и, наконец, среднее время нахождения в системе  час.
час.
3.4.3 Одноканальные СМО смешанного типа.
Предположим, что длина очереди составляет m
требований. Тогда, для любого s
£
m
, вероятность нахождения СМО в состоянии Е
1+
s
, вычисляется по формуле  , т.е. одна заявка обслуживается и еще s
заявок – в очереди.
, т.е. одна заявка обслуживается и еще s
заявок – в очереди.
Вероятность простоя системы равна  ,
,
а вероятность отказа системы -  .
.
Даны три одноканальные системы, для каждой l =5, m =6. Но первая система – с отказами, вторая – с чистым ожиданием, а третья – с ограниченной длиной очереди, m =2. Найти и сравнить вероятности простоя этих трех систем.
Решение.
Для всех систем коэффициент загрузки y
=5/6. Для системы с отказами  . Для системы с чистым ожиданием
. Для системы с чистым ожиданием  . Для системы с ограниченной длиной очереди
. Для системы с ограниченной длиной очереди  . Вывод очевиден: чем больше заявок находится в очереди, тем меньше вероятность простоя системы.
. Вывод очевиден: чем больше заявок находится в очереди, тем меньше вероятность простоя системы.
3.5 Многоканальные СМО.
3.5.1 Многоканальные СМО с отказами.
Будем рассматривать системы (Р/Е/s):(-/s/¥) в предположении, что время обслуживания не зависит от входного потока и все линии работают независимо. Многоканальные системы, помимо коэффициента загрузки, можно также характеризовать коэффициентом  , где s
– число каналов обслуживания. Исследуя многоканальные СМО, получим следующие формулы (формулы Эрлáнга
) для вероятности нахождения системы в состоянии Е
k
в случайный момент времени:
, где s
– число каналов обслуживания. Исследуя многоканальные СМО, получим следующие формулы (формулы Эрлáнга
) для вероятности нахождения системы в состоянии Е
k
в случайный момент времени:
 , k=0, 1, …
, k=0, 1, …
Функция стоимости.
Как и для одноканальных систем, увеличение коэффициента загрузки ведет к увеличению вероятности отказа системы. С другой стороны, увеличение количества линий обслуживания ведет к увеличению вероятности простоя системы или отдельных каналов. Таким образом, необходимо найти оптимальное количество каналов обслуживания данной СМО. Среднее число свободных линий обслуживания можно найти по формуле  . Введем С(s
) – функцию стоимости
СМО, зависящую от с
1
– стоимости одного отказа (штрафа за невыполненную заявку) и от с
2
– стоимости простоя одной линии за единицу времени.
. Введем С(s
) – функцию стоимости
СМО, зависящую от с
1
– стоимости одного отказа (штрафа за невыполненную заявку) и от с
2
– стоимости простоя одной линии за единицу времени.
Для поиска оптимального варианта надо найти (и это можно сделать) минимальное значение функции стоимости: С(s
) = с
1*
l
*
p
s
+с
2* , график которой представлен на рисунке 3.3:
, график которой представлен на рисунке 3.3:

Рисунок 3.3
Поиск минимального значения функции стоимости состоит в том, что мы находим ее значения сначала дляs =1, затем для s =2, потом для s =3, и т.д. до тех пор, пока на каком-то шаге значение функции С(s ) не станет больше предыдущего. Это и означает, что функция достигла своего минимума и начала расти. Ответом будет то число каналов обслуживания (значение s ), для которого функция стоимости минимальна.
ПРИМЕР.
Сколько линий обслуживания должна содержать СМО с отказами, если l =2треб/час, m =1треб/час, штраф за каждый отказ составляет 7 тыс.руб., стоимость простоя одной линии – 2 тыс.руб. в час?
Решение. y = 2/1=2. с 1 =7, с 2 =2.
Предположим, что СМО имеет два канала обслуживания, т.е. s
=2. Тогда  . Следовательно, С(2) = с
1
*l*
p
2
+с
2
*(2-
y*
(1-р
2
))
= =7*2*0.4+2*(2-2*0.6)=7.2.
. Следовательно, С(2) = с
1
*l*
p
2
+с
2
*(2-
y*
(1-р
2
))
= =7*2*0.4+2*(2-2*0.6)=7.2.
Предположим, что s
=3. Тогда  , С(3) = с
1
*l*
p
3
+с
2
*
, С(3) = с
1
*l*
p
3
+с
2
*
 =5.79.
=5.79.
Предположим, что имеется четыре канала, т.е. s
=4. Тогда  ,
,  , С(4) = с
1
*l*
p
4
+с
2
*
, С(4) = с
1
*l*
p
4
+с
2
*
 =5.71.
=5.71.
Предположим, что СМО имеет пять каналов обслуживания, т.е. s
=5. Тогда  , С(5) =
6.7 – больше предыдущего значения. Следовательно, оптимальное число каналов обслуживания – четыре.
, С(5) =
6.7 – больше предыдущего значения. Следовательно, оптимальное число каналов обслуживания – четыре.
3.5.2 Многоканальные СМО с очередью.
Будем рассматривать системы (Р/Е/s):(d/d+s/¥) в предположении, что время обслуживания не зависит от входного потока и все линии работают независимо. Будем говорить, что в системе установилсястационарный режим работы , если среднее число поступающих требований меньше среднего числа требований, обслуженных на всех линиях системы, т.е. l
P(w>0)
– вероятность ожидания начала обслуживания,  .
.
Последняя характеристика позволяет решать задачу об определении оптимального числа каналов обслуживания с таким расчетом, чтобы вероятность ожидания начала обслуживания была меньше заданного числа. Для этого достаточно просчитать вероятность ожидания последовательно при s =1, s =2, s =3 и т.д.
ПРИМЕР.
СМО – станция скорой помощи небольшого микрорайона. l =3 вызова в час, а m = 4 вызова в час для одной бригады. Сколько бригад необходимо иметь на станции, чтобы вероятность ожидания выезда была меньше 0.01?
Решение.
Коэффициент загрузки системы y
=0.75. Предположим, что в наличие имеется две бригады. Найдем вероятность ожидания начала обслуживания при s
=2.  ,
,  .
.
Предположим наличие трех бригад, т.е. s =3. По формулам получим, что р 0 =8/17, Р(w >0)=0.04>0.01 .
Предположим, что на станции четыре бригады, т.е. s =4. Тогда получим, что р 0 =416/881, Р(w >0)=0.0077<0.01 . Следовательно, на станции должно быть четыре бригады.
3.6 Вопросы для самоконтроля
- Предмет и задачи теории массового обслуживания.
- СМО, их модели и обозначения.
- Входной поток требований. Интенсивность входного потока.
- Состояние системы. Матрица и граф переходов.
- Одноканальные СМО с отказами.
- Одноканальные СМО с очередью. Характеристики.
- Стационарный режим работы. Коэффициент загрузки системы.
- Многоканальные СМО с отказами.
- Оптимизация функции стоимости.
- Многоканальные СМО с очередью. Характеристики.
3.7 Упражнения для самостоятельной работы
- Закусочная на АЗС имеет один прилавок. Автомобили прибывают в соответствии с пуассоновским распределением, в среднем 2 автомобиля за 5 минут. Для выполнения заказа в среднем достаточно 1.5 минуты, хотя продолжительность обслуживания распределена по экспоненциальному закону. Найти: а) вероятность простоя прилавка; b) средние характеристики; c) вероятность того, что количество прибывших автомобилей будет не менее 10.
- Рентгеновский аппарат позволяет обследовать в среднем 7 человек в час. Интенсивность посетителей составляет 5 человек в час. Предполагая стационарный режим работы, определить средние характеристики.
- Время обслуживания в СМО подчиняется экспоненциальному закону,
m = 7требований в час. Найти вероятность того, что а) время обслуживания находится в интервале от 3 до 30 минут; b) требование будет обслужено в течение одного часа. Воспользоваться таблицей значений функции е х . - В речном порту один причал, интенсивность входного потока – 5 судов в день. Интенсивность погрузочно-разгрузочных работ – 6 судов в день. Имея в виду стационарный режим работы, определить все средние характеристики системы.
- l =3, m =2, штраф за каждый отказ равен 5, а стоимость простоя одной линии равна 2?
- Какое оптимальное число каналов обслуживания должна иметь СМО, если l =3, m =1, штраф за каждый отказ равен 7, а стоимость простоя одной линии равна 3?
- Какое оптимальное число каналов обслуживания должна иметь СМО, если l =4, m =2, штраф за каждый отказ равен 5, а стоимость простоя одной линии равна 1?
- Определить число взлетно-посадочных полос для самолетов с учетом требования, что вероятность ожидания должна быть меньше, чем 0.05. При этом интенсивность входного потока 27 самолетов в сутки, а интенсивность их обслуживания – 30 самолетов в сутки.
- Сколько равноценных независимых конвейерных линий должен иметь цех, чтобы обеспечить ритм работы, при котором вероятность ожидания обработки изделий должна быть меньше 0.03 (каждое изделие выпускается одной линией). Известно, что интенсивность поступления заказов 30 изделий в час, а интенсивность обработки изделия одной линией – 36 изделий в час.
- Непрерывная случайная величина Х распределена по показательному закону с параметром l=5. Найти функцию распределения, характеристики и вероятность попадания с.в. Х в интервал от 0.17 до 0.28.
- Среднее число вызовов, поступающих на АТС за одну минуту, равно 3. Считая поток пуассоновским, найти вероятность того, что за 2 минуты поступит: а) два вызова; б) меньше двух вызовов; в) не менее двух вызовов.
- В ящике 17 деталей, из которых 4 – бракованные. Сборщик наугад извлекает 5 деталей. Найти вероятность того, что а) все извлеченные детали – качественные; б) среди извлеченных деталей 3 бракованных.
- Сколько каналов должна иметь СМО с отказами, если l =2треб/час, m =1треб/час, штраф за каждый отказ составляет 8т.руб., стоимость простоя одной линии – 2т.руб. в час?
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
3. Контрольная задача
1. Одноканальная СМО с отказами
Простейшей из всех задач теории массового обслуживания является модель одноканальной СМО с отказами (потерями).
При этом система массового обслуживания состоит только из одного канала (n = 1) и на нее поступает пуассоновский поток заявок с интенсивностью, зависящей, в общем случае, от времени:
Заявка, заставшая канал занятым, получает отказ и покидает систему. Обслуживание заявки продолжается в течение случайного времени, распределенного по показательному закону с параметром:
Из этого следует, что «поток обслуживания» -- простейший, с интенсивностьюЧтобы представить себе этот поток, вообразим один непрерывно занятый канал, который будет выдавать обслуженные заявки потоком с интенсивностью
Требуется найти:
1) абсолютную пропускную способность СМО (А);
2) относительную пропускную способность СМО (q).
Рассмотрим единственный канал обслуживания как физическую систему S, которая может находиться в одном из двух состояний:-- свободен,-- занят.
ГСП системы показан на рис. 5.6, а.
Рис. 5.6 ГСП для одноканальной СМО с отказами (а); график решения уравнения (5.38) (б)
Из состояниявсистему, очевидно, переводит поток заявок с интенсивностью; изв-- «поток обслуживания» с интенсивностью.
Вероятности состояний: и. Очевидно, для любого момента t:
Составим дифференциальные уравнения Колмогорова для вероятностей состояний согласно правилу, данному выше:
Из двух уравнений (5.37) одно является лишним, так каки связаны соотношением (5.36). Учитывая это, отбросим второе уравнение, а в первое подставим вместовыражение:
Поскольку в начальный момент канал свободен, уравнение следует решать при начальных условиях:= 1,=0.
Линейное дифференциальное уравнение (5.38) с одной неизвестной функциейлегко может быть решено не только для простейшего потока заявок, но и для случая, когда интенсивность этого потока со временем меняется.
Для первого случая решение есть:
Зависимость величиныот времени имеет вид, изображенный на рис. 5.6, б. В начальный момент (при t = 0) канал заведомо свободен ((0) = 1). С увеличением t вероятностьуменьшается и в пределе (при) равна. Величина, дополняющаядо единицы, изменяется так, как показано на том же рисунке.
Нетрудно убедиться, что для одноканальной СМО с отказами вероятностьесть не что иное, как относительная пропускная способность q. Действительно,есть вероятность того, что в момент t канал свободен, или вероятность того, что заявка, пришедшая в момент t, будет обслужена. Следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно
В пределе, при, когда процесс обслуживания уже установится, предельное значение относительной пропускной способности будет равно:
Зная относительную пропускную способность q, легко найти абсолютную А. Они связаны очевидным соотношением:
В пределе, при, абсолютная пропускная способность тоже установится и будет равна
Зная относительную пропускную способность системы q (вероятность того, что пришедшая в момент t заявка будет обслужена), легко найти вероятность отказа:
или среднюю часть необслуженных заявок среди поданных. При
2. Многоканальная СМО с отказами
Рассмотрим n-канальную СМО с отказами. Будем нумеровать состояния системы по числу занятых каналов (или, что в данном случае то же, по числу заявок, находящихся в системе или связанных с системой). Состояния системы:
Все каналы свободны;
Занят ровно один канал, остальные свободны;
Заняты ровно к каналов, остальные свободны;
Заняты все п каналов.
ГСП СМО представлен на рис. 5.7. Около стрелок поставлены интенсивности соответствующих потоков событий. По стрелкам слева направо систему переводит один и тот же поток -- поток заявок с интенсивностью. Если система находится в состоянии(занято к каналов) и пришла новая заявка, то система переходит в состояние
Рис. 5.7 ГСП для многоканальной СМО с отказами
Определим интенсивности потоков событий, переводящих систему по стрелкам справа налево. Пусть система находится в состоянии(занят один канал). Тогда, как только закончится обслуживание заявки, занимающей этот канал, система перейдет в; значит, поток событий, переводящий систему по стрелке, имеет интенсивность. Очевидно, если обслуживанием занято два канала, а не один, поток обслуживания, переводящий систему по стрелкебудет вдвое интенсивнее; если занято k каналов -- в к раз интенсивнее. Соответствующие интенсивности указаны у стрелок, ведущих справа налево.
Из рис. 5.7 видно, что процесс, протекающий в СМО, представляет собой частный случай процесса размножения и гибели, рассмотренного выше.
Пользуясь общими правилами, можно составить уравнения Колмогорова для вероятностей состояний:
Уравнения (5.39) называют уравнениями Эрланга. Поскольку при t = 0 система свободна, начальными условиями для их решения являются:
Интегрирование системы уравнений (5.39) в аналитическом виде довольно сложно; на практике такие системы дифференциальных уравнений обычно решаются численно и такое решение дает все вероятности состояний как функции времени.
Наибольший интерес представляют предельные вероятности состоянийхарактеризующие установившийся режим СМО (при). Для нахождения предельных вероятностей воспользуемся ранее полученными соотношениями (5.32)--(5.34), полученными для модели размножения и гибели. Согласно этим соотношениям,
В этих формулах интенсивность потока заявоки интенсивность потока обслуживании (для одного канала)не фигурируют по отдельности, а входят только своим отношением. Это отношение обозначается:
и называется приведенной интенсивностью потока заявок. Величинапредставляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.
С учетом этого обозначения, соотношения (5.40) принимают вид:
Соотношения (5.41) называются формулами Эрланга. Они выражают предельные вероятности всех состояний системы в зависимости от параметрови n.
Имея вероятности состоянийможно найти характеристики эффективности СМО: относительную пропускную способность q, абсолютную пропускную способность А и вероятность отказа.
Вероятность отказа. Заявка получает отказ, если приходит в момент, когда все и каналов заняты. Вероятность этого равна
Относительная пропускная способность. Вероятность того, что заявка будет принята к обслуживанию (относительная пропускная способность а), дополняетдо единицы:
Абсолютная пропускная способность:
Среднее число заявок в системе. Одной из важных характеристик СМО с отказами является среднее число занятых каналов (в данном случае оно совпадает со средним числом заявок, находящихся в системе). Обозначим это среднее число. Величинуможно вычислить через вероятности по формуле
как математическое ожидание дискретной случайной величины, однако проще выразить среднее число занятых каналов через абсолютную пропускную способность А, которая уже известна. Действительно, А есть не что иное, как среднее число заявок, обслуживаемых в единицу времени; один занятый канал обслуживает в среднем за единицу временизаявок; среднее число занятых каналов получится делением А на:
или, переходя к обозначению,
пропускной вероятность максимизация доход
Контрольная задача 3. Игра с природой.
Швейная фабрика выпускает детские платья и костюмы, сбыт которых зависит от состояния погоды.
Задача заключается в максимизации средней величины дохода от реализации выпущенной продукции, учитывая капризы погоды.
1) AC:1910*(13-6)+590*(44-23)=13370+12390=25760
2) AD:590*(13-6)+880*(44-23)-(1910-590)*6=(22610-1320)*6=127740
3) BC:590*(13-6)+880*(44-23)-(880-590)*23=(22610-290)*23=513360
4) BD:590*(13-6)+880*(44-23)=4130+18480=22610
Доход при теплой и при холодной погоде
25760*x+127740*(1-x)=513360*x+22610*(1-x)
25760*x+127740-127740*x=513360*x+22610-22610*x
25760*x-127740-513360*x+22610*x=22610-127740=0
592730*x=-105130/*(-1)
Рассчитаем ассортимент фабрики:
(1910+590)*0,177+(880+590)*0,823=(1910*0,177+590*0,823)+(880*0,177+590*0,823)=(338,07+485,57)+(155,76+485,57)=824платьев+641костюмов
Рассчитаем доход:
1) При теплой погоде
25760*0,177+127740*0,823=4559,52+105130,02=109689,54
2) При холодной погоде
513360*0,177+22610*0,823=90864,72+18608,03=109472,75
Ответ: 824 платьев и 641 костюмов, доход равен 109689,54 д.ед.
Список используемой литературы
1. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. Учебное пособие. М., Финансы и статистика, 2005.
2. Глухов В.В. Математические методы и модели для менеджмента: учебное пособие. СПБ; М.; Краснодар: Лань, 2005.
3. Грицюк С.Н. Математические методы и модели в экономике: учебник. Ростов н/Д: Феникс, 2007.
4. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. М., Изд-во «Дело и сервис», 2004.
5. Исследование операций в экономике. Учебное пособие для вузов/Под ред. проф. Н.Ш. Кремера. М., ЮНИТИ, 2005.
Размещено на Allbest.ru
...Подобные документы
Моделирование процесса массового обслуживания. Разнотипные каналы массового обслуживания. Решение одноканальной модели массового обслуживания с отказами. Плотность распределения длительностей обслуживания. Определение абсолютной пропускной способности.
контрольная работа , добавлен 15.03.2016
Понятие случайного процесса. Задачи теории массового обслуживания. Классификация систем массового обслуживания (СМО). Вероятностная математическая модель. Влияние случайных факторов на поведение объекта. Одноканальная и многоканальная СМО с ожиданием.
курсовая работа , добавлен 25.09.2014
Общие понятия теории массового обслуживания. Особенности моделирования систем массового обслуживания. Графы состояний СМО, уравнения, их описывающие. Общая характеристика разновидностей моделей. Анализ системы массового обслуживания супермаркета.
курсовая работа , добавлен 17.11.2009
Понятие и критерии оценивания системы массового обслуживания, определение ее типа, всех возможных состояний. Построение размеченного графа состояний. Параметры, характеризующие ее работу, интерпретация полученных характеристик, эффективность работы.
контрольная работа , добавлен 01.11.2010
Построение модели многоканальной системы массового обслуживания с ожиданием, а также использованием блоков библиотеки SimEvents. Вероятностные характеристики аудиторской фирмы как системы массового обслуживания, работающей в стационарном режиме.
лабораторная работа , добавлен 20.05.2013
Функциональные характеристики системы массового обслуживания в сфере автомобильного транспорта, ее структура и основные элементы. Количественные показатели качества функционирования системы массового обслуживания, порядок и главные этапы их определения.
лабораторная работа , добавлен 11.03.2011
Изучение теоретических аспектов эффективного построения и функционирования системы массового обслуживания, ее основные элементы, классификация, характеристика и эффективность функционирования. Моделирование системы массового обслуживания на языке GPSS.
курсовая работа , добавлен 24.09.2010
Решение системы дифференциальных уравнений методом Рунге-Кутта. Исследованы возможности применения имитационного моделирования для исследования систем массового обслуживания. Результаты моделирования базового варианта системы массового обслуживания.
лабораторная работа , добавлен 21.07.2012
Элементы теории массового обслуживания. Математическое моделирование систем массового обслуживания, их классификация. Имитационное моделирование систем массового обслуживания. Практическое применение теории, решение задачи математическими методами.
курсовая работа , добавлен 04.05.2011
Система массового обслуживания типа M/M/1, ее компоненты. Коэффициент использования обслуживающего устройства. Обозначение M/D/1 для системы массового обслуживания. Параметры и результаты моделирования систем. Среднее время ожидания заявки в очереди.
Открытие бизнеса

Где можно и где нельзя работать после туберкулеза Где можно работать после
Форекс
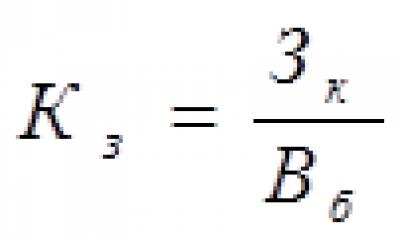
Направления повышения эффективности использования собственного капитала На базе двигателя с плоским печатным якорем разработаны изделия для автомобильной промышленности
Банки