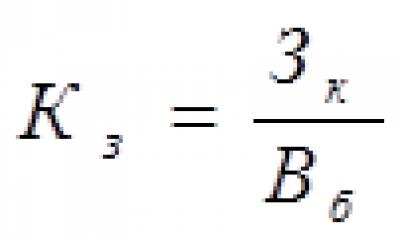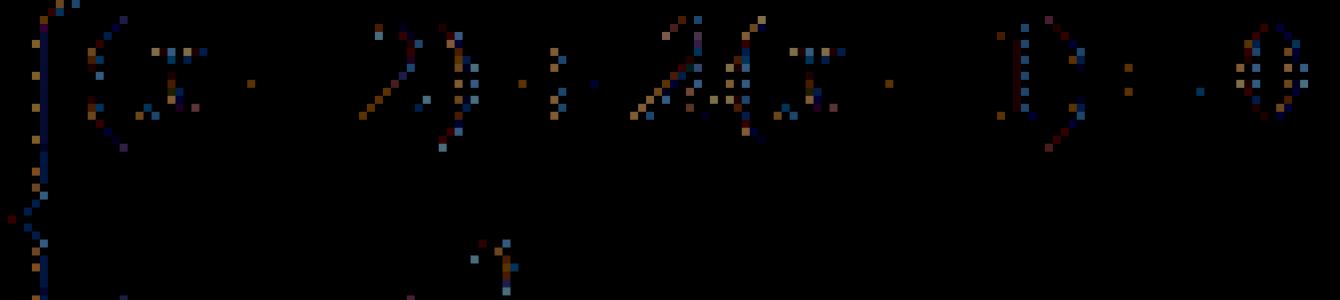Улучшенной разновидностью метода перевода менее важных критериев в ограничения является метод последовательных уступок (называемый также методом оптимизации по последовательно применяемым критериям), предлагаемый прежде всего В.

В. Подиновским в ряде работ. Его суть состоит в следующем. Проводится анализ относительной важности критериев и критерии располагаются и нумеруются в порядке убывания важности. Производится

оптимизация по первому критерию и определяется его наибольшее значение f*. Далее эксперт оценивает величину допустимого снижения (уступки) данного критерия (f1* - Af) и ищется оптимум второго по важности критерия и т.д. После оптимизации последнего по важности критерия при условии, что значение каждого критерия k = 1, K должно быть не меньше (f* - Afk), k = 1, K , получаемые решения считаются оптимальными.

Достоинства данного метода в его простоте и наглядности. Важным преимуществом является возможность целенаправленного участия лица, принимающего решения в процессе оптимизации с учетом ранее полученных (на предыдущем этапе оптимизации) данных путем выбора величины уступки по каждому критерию.

Основным теоретическим недостатком данного метода является то, что на каждом шаге происходит усечение множества точек, оптимальных по Парето, отсюда в общем случае получившееся решение не оптимально по Парето, т. е. требуется дополнительное доказательство оптимальности по Парето данного решения, что является очень сложной процедурой. Иначе придется смириться с тем, что данное решение, хотя и удовлетворяет лицо, принимающее решение значениями всех критериев, но не обязательно является оптимальным. Однако на практике это не столь важно, так как в реальной ситуации ищут, как правило, не оптимальное, но «достаточно хорошее» решение. Вторым недостатком является сложность выбора и обоснования величин уступок по отдельным критериям, так как величины уступок не соизмеримы между собой ввиду различной экономической сущности разных критериев. Однако от второго недостатка можно избавиться применением нормализации критериев.

Еще по теме Метод уступок:

Порядок признания доходов при методе начисления и кассовом методе
3. Метод дисконтированных денежных потоков: сущность метода, основные этапы оценки
метод цепных подстановок с использованием индексов (индексный метод).
5.6. Корректировка при переходе от метода ЛИФО к методу ФИФО
15.6. Метод калькулирования сокращенной себестоимости продукции (метод директ-костинга)
3. Метод стоимости розничных продаж и метод обследований семейных бюджетов
7.3. Комплексные методы учета влияния инфляции на показатели бухгалтерской отчетности. Метод восстановительной стоимости

Встречаются случаи, когда пользователь готов на некоторое снижение величин более важных критериев, чтобы повысить величину менее важных. В таких ситуациях можно воспользоваться методом уступок . Идею этого метода можно изложить следующим образом.

Метод последовательных уступок. Согласно этому методу локальные критерии предварительно ранжируются по важности. Затем ищется наилучшее решение по наиболее важному критерию. На следующем шаге ищется решение наилучшее по следующему по важности критерию, причем допускается потеря в значении первого критерия не более чем на некоторую обусловленную величину, т.е. делается уступка по первому критерию. На третьем шаге оптимизируется решение по третьему критерию, при заданных уступках по первому и второму и т.д., пока не будет рассмотрен последний по важности критерий. При решении многокритериальных задач методом последовательных уступок вначале нужно определить важность частных критериев, т.е. расположить частные критерии в порядке убывания важности. Таким образом, главным считается критерий F 1 , менее важным F 2 , . . . , F m . Минимизируется первый по важности критерий и определяется его наименьшее значение F 1 min . Затем назначается величина допустимого снижения уступки D 1 ³0 критерия F 1 и ищется наименьшее значение критерия F 2 при условии, что значение F 1 должно быть не больше, чем F 1 min +D 1 . Снова назначается уступка D 2 ³0, но уже по второму критерию, которая вместе с первой используется при нахождении условного минимума F 3 и т.д. Наконец, минимизируется последний по важности критерий F m при условии, что значения каждого критерия F i из m-1 предыдущих должны быть не больше соответствующей величины F i min +D i .Получаемое в итоге решение считается оптимальным.

Таким образом, оптимальным считается всякое решение, являющимся решением последней задачи из следующей последовательности задач

1) Найти F 1 min =min F 1 (X)

2) Найти F 2 min .=min F 2 (X) (1)

F 1 £ F 1 min +D 1

m) Найти F m min .=min F m (X)

F i £ F imin +D i

i=1,2, . . . ,m-1

Величины уступок выбирают в пределах инженерной точности, т.е. 5-10% от наименьшего значения критерия.

Пример. Пусть в области D={0;4} заданы два критерия F 1 (x)=(x-1) 2 +1 F 2 (x)=(x-2) 2 +2, которые нужно минимизировать (рис.1). Критерий F 1 важнее критерия F 2 (F 1 предпочтительнее F 2).

Рис.1. Графики функций F 1 и F 2

1. Согласно алгоритму минимизируем первый по важности критерий, и определяется его наименьшее значение F 1 min .Формулируем задачу оптимизации

найти min F 1 (x)= min[(x-1) 2 +1]

при ограничениях

Минимум для первого критерия достигается в точке x 1 opt =1 и равен F 1 (x 1 opt)=1

2. Затем назначается величина уступки D 1 =0.1 критерия F 1 и ищется наименьшее значение критерия F 2 при условии, что значение F 1 должно быть не больше, чем F 1 min +D 1 . Таким образом, мы получили следующую задачу оптимизации

minF 2 (x)=min[(x-2) 2 +2]

при ограничениях

(x-1) 2 +1£1+0.1

Для решения воспользуемся методом множителей Лагранжа. В результате получим безусловную задачу оптимизации

Ф(x, λ)= (x-2) 2 +2+ λ((x-1) 2 -0.1).

Находим частные производные и приравниваем их к нулю. В результате получим систему уравнений

Решая эту систему, получим x 2 opt =1.32.

Согласно алгоритму, решение, полученное на последнем этапе, и будет считаться оптимальным, т.е. x opt =1.32.

Решим данную задачу, используя систему MathCad.

f(x):=(x-2) 2 +2 целевая функция

x:=1 начальное приближение

Прежде всего отметим, что метод последовательных уступок решения многокритериальных задач оптимизации применяется в случае, когда частные критерии могут быть упорядочены в порядке убывающей важности. А именно, пусть - наиболее важный, - наименее важный среди всех N рассматриваемых частных критериев. Далее считаем, что такое упорядочение имеющихся в задаче многокритериальной оптимизации частных критериев уже реализовано. Суть этого метода состоит в реализации следующих этапов.

На первом этапе решается однокритериальная задача для первого наиболее важного критерия:

при условии .

Пусть - минимальное значение целевой функции для однокритериальной задачи, решенной на первом этапе. По завершению первого этапа исходя из практических соображений и принятой точности назначается некоторая уступка ∆ 1 (∆ 1 > 0), которую можно допустить в рамках реализации этого метода с учетом особенностей критерия по отношению к найденному значению , чтобы перейти ко второму этапу - минимизации следующего по важности частного критерия. При этом на критерий налагается требование, согласно которому его оценка не должна превышать допустимой величины (именно здесь учитывается назначенная уступка), что реализуется в качестве соответствующего ограничения на следующем этапе метода.

А именно, на втором этапе метода последовательных уступок ищем решение, минимизирующее g (2) (x) при указанном ограничении на при указанном ограничении на и с учетом заданного множества X допустимых решений, т.е. решаем следующую однокритериальную задачу:

при ограничениях

Аналогичные процедуры реализуются на всех последующих этапах этого метода. В частности, на k -ом этапе решается соответствующая однокритериальная задача для k -го по важности частного критерия с учетом заданного множества X допустимых решений и всех ранее наложенных ограничений, к которым добавляется еще одно требование, согласно которому оценка для частного критерия, минимизируемого на предыдущем (k-1)- ом этапе не должна превышать величины ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/>"> где -минимальное значение целевой функции предыдущего (k-1)- гo этапа, а - соответствующая уступка (), которая была принята в качестве допустимой по отношению к найденному значению , чтобы перейти к рассматриваемому k -му этапу реализации метода. А именно, решается задача:

при ограничениях

Таким образом, для многокритериальной задачи с N частными критериями последовательно реализуется N указанных этапов. Решение, получаемое на последнем этапе, принимается в качестве наилучшего решения исходной многокритериальной задачи оптимизации в рамках этого метода.

Необходимо отметить, что метод последовательных уступок может приводить к решениям, не принадлежащим переговорному множеству решений, оптимальных по Парето. Другими словами, найденное решение может не быть эффективным.

Метод идеальной точки

На содержательном уровне соответствующий подход к решению многокритериальной задачи оптимизации во множестве допустимых решений (на границе Парето), называемый методом идеальной точки, состоит в нахождении точки, дающей решение, ближайшее к так называемой утопической точке, которую, обычно, задает лицо, принимающее решение (ЛПР), в виде желаемых значений показателей всех частных критериев. При этом, как правило, ЛПР выбирает на практике сочетание наилучших значений всех имеющихся частных критериев и такая задаваемая утопическая точка не реализуется при заданных ограничениях для допустимых решений, - отсюда и соответствующее ее название (в противном случае множество абсолютных решений оказалось бы не пустым и соответствующая задача оптимизации решалась бы более простыми методами). Найденную точку с указанным свойством и принимают в качестве наилучшего решения по методу идеальной точки. Приведем формальное представление этого метода. Пусть

где, напомним, - частные критерии соответствующей задачи многокритериальной оптимизации. Кроме того, пусть - наилучшие (т.е. минимальные - в соответствующих задачах минимизации частных критериев) значения этих критериев в заданной области допустимых решений .

Тогда в пространстве точку с координатами называют утопической точкой - УТ (еще раз подчеркнем, что, как правило, в задачах многокритериальной оптимизации такая точка не реализуется в заданной области допустимых решений ).

Кроме того, ближайшую (по расстоянию в метрике соответствующего пространства) к УТ точку в пространстве , которую можно реализовать при заданных ограничениях , называют идеальной точкой - ИТ. При этом точка х = (х, у, ... , z) в заданной области допустимых решений , которая дает решение, соответствующее в пространстве идеальной точке, как раз и выбирается в качестве ответа для исходной многокритериальной задачи оптимизации.

В общем случае, метод идеальной точки может приводить к решениям, не принадлежащим границе Парето.

Методы компенсации

Эта группа методов использует идею возможного компромисса между противоречивыми оценками по паре (или по группам) критериев исходной многокритериальной задачи. Образно говоря, для каждой анализируемой альтернативы на одной чаше «весов сравнения» отмечаются достоинства оценок (по некоторой группе критериев), а на другой - недостатки (по другой группе критериев). При этом ЛПР находит соответствующие возможности компромисса в рамках таких сравнений. После этого задача выбора альтернатив (с учетом найденных компромиссов для каждой из них) значительно упрощается.

Суть такой идеи была изложена еще в 1752 г. Франклином Б. Он отмечает, что «при сравнении трудно держать в голове все достоинства и недостатки каждой из альтернатив». Поэтому он составляет два отдельных списка из достоинств и недостатков альтернативы. Затем после тщательного анализа определяет, какой недостаток (или их совокупность) можно считать эквивалентным определенному достоинству (или их совокупности). После чего такие «компромиссные» достоинства и недостатки вычеркиваются из списков.

Метод главного критерия

Методы последовательной оптимизации

Недостатки свёртывания нескольких критериев заставляют искать другие подходы к решению задач многокритериального выбора. В данной лекции мы будем рассматривать методы последовательной оптимизации.

К методам последовательной оптимизации относят метод последовательных уступок и как частный случай данного метода – метод главного критерия , лексикографический критерий и метод равенства частных критериев .

Существует один, часто применяемый способ свести многокритериальную задачу к однокритериальной – это выделить один (главный, основной) критерий F 1 и стремиться его обратить в максимум (минимум), а на остальные F 2 , F 3 , . . Fm частные критерии наложить только некоторые ограничения, потребовав, чтобы они были не меньше (больше) каких-то заданных величин. Таким образом, идея метода главного критерия заключается в том, что частные критерии обычно неравнозначны между собой (одни из них более важны, чем другие) и это позволяет выделит главный критерий, а остальные (критерии) рассматривать как дополнительные, сопутствующие. Например, при оптимизации плана работы предприятия можно потребовать, чтобы прибыль была максимальна, план по ассортименту – выполнен или перевыполнен, а себестоимость продукции – не выше заданной. При таком подходе все показатели, кроме одного – главного, переводятся в разряд ограничений. Такое различие позволяет сформулировать задачу многокритериальной оптимизации как задачу нахождения условного экстремума основного (главного) критерия:

1) Найти F 1 min =min F 1 (X)

2) Найти F 2 min .=min F 2 (X) (1)

F 1 £ F 1 min +D 1

m) Найти F m min .=min F m (X)

F i £ F imin +D i

i=1,2, . . . ,m-1

Величины уступок выбирают в пределах инженерной точности, т.е. 5-10% от наименьшего значения критерия.

Рис.1. Графики функций F 1 и F 2

найти min F 1 (x)= min[(x-1) 2 +1]

при ограничениях

Минимум для первого критерия достигается в точке x 1 opt =1 и равен F 1 (x 1 opt)=1

minF 2 (x)=min[(x-2) 2 +2]

при ограничениях

(x-1) 2 +1£1+0.1

Ф(x, λ)= (x-2) 2 +2+ λ((x-1) 2 -0.1).

Находим частные производные и приравниваем их к нулю. В результате получим систему уравнений

Решая эту систему, получим x 2 opt =1.32.

Согласно алгоритму, решение, полученное на последнем этапе, и будет считаться оптимальным, т.е. x opt =1.32.

Решим данную задачу, используя систему MathCad.

f(x):=(x-2) 2 +2 целевая функция

x:=1 начальное приближение

ограничения

0≤x≤4

p:=Minimize(f,x) p=1.316.

Ответ: x opt =1.32.

Зам. Метод последовательных уступок целесообразно применять для решения тех инженерных задач, в которых все частные критерии упорядочены по степени важности, причём каждый критерий настолько более важен, чем последующий, что можно ограничиться учётом только попарной связи критериев и выбирать величину допустимого снижения очередного критерия с учётом поведения лишь одного следующего критерия.

Недостатком метода являются трудности с назначением и согласованием величин уступок, возрастающие с ростом размерности векторного критерия, а также необходимость формированиянеизменного для всей задачи априорного ранжирования критериев.

Как видим, в методе уступок предполагается, что разница в важности критериев не слишком велика. Можно предположить, что величина уступок как-то связана с нашим ощущением этой разницы.

Метод (последовательных) уступок заключается в анализе точек на границе Парето и выбора одной из них - компромиссной.

Назначение сервиса . Сервис предназначен для онлайн решения многокритериальных задач оптимизации методом последовательных уступок .

Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word и Excel .

При этом ограничения типа x i ≥ 0 не учитывайте. Если в задании для некоторых x i отсутствуют ограничения, то ЗЛП необходимо привести к КЗЛП, или воспользоваться этим сервисом .

Вместе с этим калькулятором также используют следующие:
Графический метод решения ЗЛП

Решение транспортной задачи

Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.

Экстремум функции двух переменных

Задачи динамического программирования
Распределить 5 однородных партий товара между тремя рынками так, чтобы получить максимальный доход от их продажи. Доход от продажи на каждом рынке G(X) зависит от количества реализованных партий товара Х и представлен в таблице.

Объем товара Х (в партиях)	Доход G(X)
Объем товара Х (в партиях)	1	2	3
0	0	0	0
1	28	30	32
2	41	42	45
3	50	55	48
4	62	64	60
5	76	76	72

Алгоритм метода последовательных уступок (компромиссов)

Вначале производится качественный анализ относительной важности критериев. На основании такого анализа критерии нумеруются в порядке убывания важности.
Ищем максимальное значение f 1 * первого критерия f=f 1 (x) на всем множестве допустимых решений. Затем назначаем величину «допустимого» снижения (уступки ) Δ 1 критерия f 1 (x) и определяем наибольшее значение f 2 * второго критерия f=f 2 (x) при условии, что значение первого критерия должно быть не меньше, чем f 1 (x)-Δ 1 . Затем назначаем величину «допустимого» снижения (уступки ) Δ 2 критерия f 2 (x) и определяем наибольшее значение f 3 * третьего критерия f=f 3 (x) при условии, что значение второго критерия должно быть не меньше, чем f 2 * - Δ 2 и т. д. Таким образом, оптимальным решением многокритериальной задачи считается всякое решение последней из задач последовательности:
1) найти max f 1 (x)=f 1 * в области x ∈ X;
2) найти max f 2 (x)=f 2 * в области, задаваемой условиями x ∈ X; f 1 (x) ≥ f 1 * -Δ 1 (6)
……………………………………………………………….
m) найти max f m (x)=f m * в области, задаваемой условиями
x ∈ X; f i (x) ≥ f i * -Δ i , i=1,...,m-1
Очевидно, что если все Δ i =0, то метод уступок находит только лексикографически оптимальные решения, которые доставляют первому по важности критерию наибольшее на Х значение. В другом крайнем случае, когда величины уступок очень велики, решения, получаемые по этому методу, доставляют последнему по важности критерию наибольшее на Х значение. Поэтому величины уступок можно рассматривать как своеобразную меру отклонения приоритета частных критериев от жесткого лексикографического.
Метод последовательных уступок не всегда приводит к получению только эффективных точек, но среди этих точек всегда существует хотя бы одна эффективная. Это следует из следующих утверждений.
Утверждение 3 . Если X ⊂ R n - множество замкнутое и ограниченное, а функции f i (x) непрерывны, то решением m-й задачи из (6) является, по крайней мере, одна эффективная точка.
Утверждение 4 . Если x * - единственная (с точностью до эквивалентности) точка, являющаяся решением m-й задачи из (6), то она эффективна.

Примеры решения многокритериальной задачи методом последовательных уступок

Пример №1 . Решить методом последовательных уступок многокритериальную задачу.
f 1 (x)=7x 1 +2x 3 -x 4 +x 5 → max ,

при ограничениях
-x 1 +x 2 +x 3 =2 ;
3x 1 -x 2 +x 4 =3 ;
5x 1 +2x 2 +x 3 +x 4 +x 5 =11;
x i ≥ 0 для i=1,2,...,5.
Упорядочим критерии согласно их нумерации, то есть будем в начале работать с критерием f 1 (x), а затем с критерием f 2 (x).
При решении примера методом искусственного базиса была получена симплекс-таблица (табл.). Возьмем ее в качестве начальной, вычислив относительные оценки для функции f=f 1 (x). Получим таблицу 10. Таблица 11 определяет точку, доставляющую функции f1(x) наибольшее значение f 1 * , равное 16.
Таблица 10. Таблица 11.

		7	0
c в		X 1	x 2			x 4	x 2
2	x 3	-1	1	2	x 3	1/3	2/3	3
-1	x 4	3	-1	3	x 1	1/3	-1/3	1
1	x 5	3	2	6	x 5	-1	3	3
	f 1	-9	5	7	f 1	3	2	16

Далее переходим к решению задачи
f 2 (x)=x 1 -5x 2 -4x 3 +x 4 → max
при ограничениях задачи, к которым добавлено новое ограничение f 1 (x)≥f 1 * -Δ:
-x 1 +x 2 +x 3 =2,
3x 1 -x 2 +x 4 =3 , (7)
5x 1 +2x 2 +x 3 +x 4 +x 5 =11,
7x 1 +2x 3 - x 4 +x 5 ³16-Δ,
x i ≥ 0 для i=1,2,...,5.
Новое ограничение преобразуем в равенство и заменим переменные x 1 , x 3, x 5 , используя таблицу 11, выражениями
x 1 =1/3x 2 -1/3x 4 +1, x 3 =-2/3x 2 -1/3x 4 +3, x 5 =-3x 2 +x 4 +3.
В результате этих преобразований дополнительно введенное ограничение примет вид -2x 2 -x 4 +x 6 =-16+Δ. Итак, получили задачу параметрического программирования с параметром в правой части ограничений.
В качестве начальной таблицы для задачи (7) можно использовать таблицу 12, которая получена из таблицы 11 в результате пополнения ее еще одной строкой и пересчета строки относительных оценок. Решим задачу (7) для произвольного параметра Δ≥0. Для этого столбец правых частей ограничений в таблице 12 представим в виде двух столбцов z′, z″: z i 0 =z i ′+z i ″Δ. При выборе главной строки в таблице 12 следует использовать значения из столбца z′. Полученная далее таблица 13 является оптимальной при Δ=0 и при всех значениях Δ, удовлетворяющих условиям
3+(-1/9) Δ ≥ 0, 1+(-1/9) Δ ≥ 0, 3+1/3 Δ ≥ 0, 0+1/3 Δ ≥ 0.
Из этой системы неравенств получаем 0 ≤ Δ ≤ 9. При этих значениях параметра решением задачи является точка x*=(1+(-1/9)Δ, 0, 3+(-1/9)Δ, 0+1/3Δ, 3+1/3Δ).
Таблица 12. Таблица 13.

		1	-5
с в		x 4	x 2	z′	z″		x 6	x 2	z′	z″
-4	x 3	1/3	2/3	3	0	x 3	-1/9	4/9	3	-1/9
1	x 1	1/3	-1/3	1	0	x 1	-1/9	-5/9	1	-1/9
0	x 5	-1	3	3	0	x 5	1/3	11/3	3	1/3
0	x 6	3	2	0	1	x 4	1/3	2/3	0	1/3
	f 2	-2	2	-11	0	f 2	2/3	10/3	-11	2/3

При Δ > 9 таблица 13 не является оптимальной, и нужно выполнить шаг двойственного симплекс-метода с главным элементом, стоящим на пересечение второй строки и первого или второго столбцов. Получим таблицу 14, из которой видно, что при Δ > 9 решениями являются точки, доставляющие функции f 2 (x) значение –5. Таблица 14 определяет опорное решение x ** =(0,0,2,3,6).
Таблица 14.

	x 1	x 2	z′	z″
x 3	-1	1	2	0
x 6	-9	5	-9	1
x 5	3	2	6	0
x 4	3	-1	3	0
f 2	6	0	-5	0

Найдем эти решения. Выберем главным столбец с 0-оценкой. В зависимости от Δ главной строкой будет первая или вторая строка. Если
(-9+Δ)/5 > 2, то главной строкой будет выбрана 1-я. А значит, следующей будет таблица 15. Она определяет опорное решение X=(0,2,0,5,2) , если
–19+Δ≥0. Итак, если D≥19, оптимальными решениями будут все точки выпуклой комбинации
ax ** +(1-a)x * =(0, 2-2a, 2a,5-2a,2+4a), где a∈.
Таблица 15.

	x 1	x 3	z′	z″
x 2	-1	1	2	0
x 6	-4	-5	-19	1
x 5	5	-2	2	0
x 4	2	1	5	0
f 2	6	0	-5	0

Если (-9+Δ)/5 > 2, то главной строкой будет выбрана 2-я. А значит, следующей после таблицы 14 будет таблица 16. Таблица 16 определяет решение X=(0, (-9+Δ)/5, (19-Δ)/5, (6+Δ)/5, (48-2Δ)/5), если –19+Δ≤0. Итак, если Δ≤19, оптимальными решениями будут все точки выпуклой комбинации
ax**+(1-a)x*=(0, (1-a)(-9+Δ)/5, (19-Δ)/5+a(-9+Δ)/5, (6+Δ)/5+a(9-Δ)/5, (48-2Δ)/5+a(-18+2Δ)/5), где a∈.
Таблица 16.

	x 1	x 6	z′	z″
x 3	4/5	-1/5	19/5	-1/5
x 2	-9/5	1/5	-9/5	1/5
x 5	33/5	-2/5	48/5	-2/5
x 4	6/5	1/5	6/5	1/5
f 2	6	0	-5	0

Окончательный результат формулируется следующим образом: решением многокритериальной задачи являются:
точки x*=(1+(-1/9)Δ, 0, 3+(-1/9)Δ, 0+1/3Δ, 3+1/3Δ), если 0 ≤ Δ ≤ 9,
точки x**=(0, (1-a)(-9+Δ)/5, (19-Δ)/5+a(-9+Δ)/5,
(6+Δ)/5+a(9-Δ)/5,(48-2Δ)/5+a(-18+2Δ)/5), если 9 < Δ ≤ 19,
точки x *** =(0, 2-2a, 2a,5-2a,2+4a), если Δ ≥ 19,
где a∈.

Пример №2 . Методом последовательных уступок найти решение задачи, считая, что критерии упорядочены по важности в последовательности {f 2 ,f 1 }, и Δ 2 =1.
f 1 =-x 1 +3x 2 → max,
f 2 (x)=4x 1 -x 2 → max ,
Первая задача из последовательности (6) в данном случае имеет вид:
f 2 (x)=4x 1 -x 2 → max ,
при ограничениях
-x 1 +x 2 ≤1, x 1 +x 2 ≥3, x 1 -2x 2 ≤0 , x 1 ≤4 , x 2 ≤3.
Решение этой задачи можно найти графически. Из рисунка 14 видно, что максимум критерия f 2 (x) на множестве X достигается в вершине x 5 =(4,2) и f 2 * =f 2 (x 5)=14.
Графическое решение примера №2.

Рис.
Добавим к ограничениям задачи условие f 2 ≥f 2 * -Δ и сформулируем вторую задачу последовательности (6):
f 1 =-x 1 +3x 2 → max,
-x 1 +x 2 1 , x 1 +x 2 3, x 1 -2x 2 0 , x 1 4 , x 2 3,
4x 1 -x 2 13
Ее решением (рис.) будет вершина x 4 =(4,3) и f 1 * =f 1 (x 4)=5. Так как, оптимальное решение последней задачи единственно, то в силу утверждения 5, x 4 принадлежит множеству Парето.
Отметим, что при Δ∈ методом последовательных уступок будет найдена одна из точек отрезка , а при Δ>1, одна из точек отрезка . Все эти точки и только они принадлежит множеству Парето.