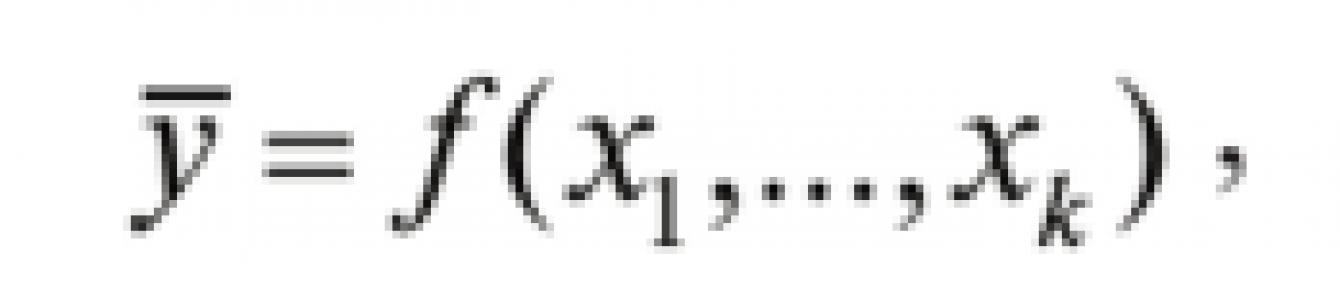Регрессионный анализ лежит в основе создания большинства эконометрических моделей, к числу которых следует отнести и модели оценки стоимости. Для построения моделей оценки этот метод можно использовать, если количество аналогов (сопоставимых объектов) и количество факторов стоимости (элементов сравнения) соотносятся между собой следующим образом: п > (5 -г-10) х к, т.е. аналогов должно быть в 5-10 раз больше, чем факторов стоимости. Это же требование к соотношению количества данных и количества факторов распространяется и на другие задачи: установление связи между стоимостью и потребительскими параметрами объекта; обоснование порядка расчета корректирующих индексов; выяснение трендов цен; установление связи между износом и изменениями влияющих факторов; получение зависимостей для расчета нормативов затрат и т.п. Выполнение данного требования необходимо для того, чтобы уменьшить вероятность работы с выборкой данных, которая не удовлетворяет требованию нормальности распределения случайных величин.

Регрессионная связь отражает лишь усредненную тенденцию изменения результирующей переменной, например, стоимости, от изменения одной или нескольких факторных переменных, например, местоположения, количества комнат, площади, этажа и т.п. В этом заключается отличие регрессионной связи от функциональной, при которой значение результирующей переменной строго определено при заданном значении факторных переменных.

Наличие регрессионной связи / между результирующей у и факторными переменными х р ..., х к (факторами) свидетельствует о том, что эта связь определяется не только влиянием отобранных факторных переменных, но и влиянием переменных, одни из которых вообще неизвестны, другие не поддаются оценке и учету:

Влияние неучтенных переменных обозначается вторым слагаемым данного уравнения ?, которое называют ошибкой аппроксимации.

Различают следующие типы регрессионных зависимостей:

• ? парная регрессия - связь между двумя переменными (результирующей и факторной);
• ? множественная регрессия - зависимость одной результирующей переменной и двух или более факторных переменных, включенных в исследование.

Основная задача регрессионного анализа - количественное определение тесноты связи между переменными (при парной регрессии) и множеством переменных (при множественной регрессии). Теснота связи количественно выражается коэффициентом корреляции.

Применение регрессионного анализа позволяет установить закономерность влияния основных факторов (гедонистических характеристик ) на изучаемый показатель как в их совокупности, так и каждого из них в отдельности. С помощью регрессионного анализа, как метода математической статистики, удается, во-первых, найти и описать форму аналитической зависимости результирующей (искомой) переменной от факторных и, во-вторых, оценить тесноту этой зависимости.

Благодаря решению первой задачи получают математическую регрессионную модель, с помощью которой затем рассчитывают искомый показатель при заданных значениях факторов. Решение второй задачи позволяет установить надежность рассчитанного результата.

Таким образом, регрессионный анализ можно определить как совокупность формальных (математических) процедур, предназначенных для измерения тесноты, направления и аналитического выражения формы связи между результирующей и факторными переменными, т.е. на выходе такого анализа должна быть структурно и количественно определенная статистическая модель вида:

где у - среднее значение результирующей переменной (искомого показателя, например, стоимости, аренды, ставки капитализации) по п ее наблюдениям; х - значение факторной переменной (/-й фактор стоимости); к - количество факторных переменных.

Функция f(x l ,...,x lc), описывающая зависимость результирующей переменной от факторных, называется уравнением (функцией) регрессии. Термин «регрессия» (regression (лат.) - отступление, возврат к чему-либо) связан со спецификой одной из конкретных задач, решенных на стадии становления метода, и в настоящее время не отражает всей сущности метода, но продолжает применяться.

Регрессионный анализ в общем случае включает следующие этапы:

• ? формирование выборки однородных объектов и сбор исходной информации об этих объектах;
• ? отбор основных факторов, влияющих на результирующую переменную;
• ? проверка выборки на нормальность с использованием х 2 или биноминального критерия;
• ? принятие гипотезы о форме связи;
• ? математическую обработку данных;
• ? получение регрессионной модели;
• ? оценку ее статистических показателей;
• ? поверочные расчеты с помощью регрессионной модели;
• ? анализ результатов.

Указанная последовательность операций имеет место при исследовании как парной связи между факторной переменной и одной результирующей, так и множественной связи между результирующей переменной и несколькими факторными.

Применение регрессионного анализа предъявляет к исходной информации определенные требования:

• ? статистическая выборка объектов должна быть однородной в функциональном и конструктивно-технологическом отношениях;
• ? достаточно многочисленной;
• ? исследуемый стоимостной показатель - результирующая переменная (цена, себестоимость, затраты) - должен быть приведен к одним условиям его исчисления у всех объектов в выборке;
• ? факторные переменные должны быть измерены достаточно точно;
• ? факторные переменные должны быть независимы либо минимально зависимы.

Требования однородности и полноты выборки находятся в противоречии: чем жестче ведут отбор объектов по их однородности, тем меньше получают выборку, и, наоборот, для укрупнения выборки приходится включать в нее не очень схожие между собой объекты.

После того как собраны данные по группе однородных объектов, проводят их анализ для установления формы связи между результирующей и факторными переменными в виде теоретической линии регрессии. Процесс нахождения теоретической линии регрессии заключается в обоснованном выборе аппроксимирующей кривой и расчете коэффициентов ее уравнения. Линия регрессии представляет собой плавную кривую (в частном случае прямую), описывающую с помощью математической функции общую тенденцию исследуемой зависимости и сглаживающую незакономерные, случайные выбросы от влияния побочных факторов.

Для отображения парных регрессионных зависимостей в задачах по оценке чаще всего используют следующие функции: линейную - у - а 0 + арс + с степенную - у - aj&i + с показательную - у - линейно-показательную - у - а 0 + ар* + с. Здесь - е ошибка аппроксимации, обусловленная действием неучтенных случайных факторов.

В этих функциях у - результирующая переменная; х - факторная переменная (фактор); а 0 , а р а 2 - параметры регрессионной модели, коэффициенты регрессии.

Линейно-показательная модель относится к классу так называемых гибридных моделей вида:

где

где х (i = 1, /) - значения факторов;

b t (i = 0, /) - коэффициенты регрессионного уравнения.

В данном уравнении составляющие А, В и Z соответствуют стоимости отдельных составляющих оцениваемого актива, например, стоимости земельного участка и стоимости улучшений, а параметр Q является общим. Он предназначен для корректировки стоимости всех составляющих оцениваемого актива на общий фактор влияния, например, местоположение.

Значения факторов, находящихся в степени соответствующих коэффициентов, представляют собой бинарные переменные (0 или 1). Факторы, находящиеся в основании степени, - дискретные или непрерывные переменные.

Факторы, связанные с коэффициентами знаком умножения, также являются непрерывными или дискретными.

Спецификация осуществляется, как правило, с использованием эмпирического подхода и включает два этапа:

• ? нанесение на график точек регрессионного поля;
• ? графический (визуальный) анализ вида возможной аппроксимирующей кривой.

Тип кривой регрессии не всегда можно выбрать сразу. Для его определения сначала наносят на график точки регрессионного поля по исходным данным. Затем визуально проводят линию по положению точек, стремясь выяснить качественную закономерность связи: равномерный рост или равномерное снижение, рост (снижение) с возрастанием (убыванием) темпа динамики, плавное приближение к некоторому уровню.

Этот эмпирический подход дополняют логическим анализом, отталкиваясь от уже известных представлений об экономической и физической природе исследуемых факторов и их взаимовлияния.

Например, известно, что зависимости результирующих переменных - экономических показателей (цены, аренды) от ряда факторных переменных - ценообразующих факторов (расстояния от центра поселения, площади и др.) имеют нелинейный характер, и достаточно строго их можно описать степенной, экспоненциальной или квадратичной функциями. Но при небольших диапазонах изменения факторов приемлемые результаты можно получить и с помощью линейной функции.

Если все же невозможно сразу сделать уверенный выбор какой- либо одной функции, то отбирают две-три функции, рассчитывают их параметры и далее, используя соответствующие критерии тесноты связи, окончательно выбирают функцию.

В теории регрессионный процесс нахождения формы кривой называется спецификацией модели, а ее коэффициентов - калибровкой модели.

Если обнаружено, что результирующая переменная у зависит от нескольких факторных переменных (факторов) х { , х 2 , ..., х к, то прибегают к построению множественной регрессионной модели. Обычно при этом используют три формы множественной связи: линейную - у - а 0 + а х х х + а^х 2 + ... + а к х к, показательную - у - а 0 a *i а х т- а х ь, степенную - у - а 0 х х ix 2 a 2. .х^или их комбинации.

Показательная и степенная функции более универсальны, так как аппроксимируют нелинейные связи, каковыми и является большинство исследуемых в оценке зависимостей. Кроме того, они могут быть применены при оценке объектов и в методе статистического моделирования при массовой оценке, и в методе прямого сравнения в индивидуальной оценке при установлении корректирующих коэффициентов.

На этапе калибровки параметры регрессионной модели рассчитывают методом наименьших квадратов, суть которого состоит в том, что сумма квадратов отклонений вычисленных значений результирующей переменной у ., т.е. рассчитанных по выбранному уравнению связи, от фактических значений должна быть минимальной:

Значения j) (. и у. известны, поэтому Q является функцией только коэффициентов уравнения. Для отыскания минимума S нужно взять частные производные Q по коэффициентам уравнения и приравнять их к нулю:

В результате получаем систему нормальных уравнений, число которых равно числу определяемых коэффициентов искомого уравнения регрессии.

Положим, нужно найти коэффициенты линейного уравнения у - а 0 + арс. Сумма квадратов отклонений имеет вид:

/=1

Дифференцируют функцию Q по неизвестным коэффициентам а 0 и и приравнивают частные производные к нулю:

После преобразований получают:

где п - количество исходных фактических значений у их (количество аналогов).

Приведенный порядок расчета коэффициентов регрессионного уравнения применим и для нелинейных зависимостей, если эти зависимости можно линеаризовать, т.е. привести к линейной форме с помощью замены переменных. Степенная и показательная функции после логарифмирования и соответствующей замены переменных приобретают линейную форму. Например, степенная функция после логарифмирования приобретает вид: In у = 1пя 0 +а х 1пх. После замены переменных Y- In у, Л 0 - In а № X- In х получаем линейную функцию

Y=A 0 + cijX, коэффициенты которой находят описанным выше способом.

Метод наименьших квадратов применяют и для расчета коэффициентов множественной регрессионной модели. Так, система нормальных уравнений для расчета линейной функции с двумя переменными Xj и х 2 после ряда преобразований имеет следующий вид:

Обычно данную систему уравнений решают, используя методы линейной алгебры. Множественную степенную функцию приводят к линейной форме путем логарифмирования и замены переменных таким же образом, как и парную степенную функцию.

При использовании гибридных моделей коэффициенты множественной регрессии находятся с использованием численных процедур метода последовательных приближений.

Чтобы сделать окончательный выбор из нескольких регрессионных уравнений, необходимо проверить каждое уравнение на тесноту связи, которая измеряется коэффициентом корреляции, дисперсией и коэффициентом вариации. Для оценки можно использовать также критерии Стьюдента и Фишера. Чем большую тесноту связи обнаруживает кривая, тем она более предпочтительна при прочих равных условиях.

Если решается задача такого класса, когда надо установить зависимость стоимостного показателя от факторов стоимости, то понятно стремление учесть как можно больше влияющих факторов и построить тем самым более точную множественную регрессионную модель. Однако расширению числа факторов препятствуют два объективных ограничения. Во-первых, для построения множественной регрессионной модели требуется значительно более объемная выборка объектов, чем для построения парной модели. Принято считать, что количество объектов в выборке должно превышать количество п факторов, по крайней мере, в 5-10 раз. Отсюда следует, что для построения модели с тремя влияющими факторами надо собрать выборку примерно из 20 объектов с разным набором значений факторов. Во-вторых, отбираемые для модели факторы в своем влиянии на стоимостный показатель должны быть достаточно независимы друг от друга. Это обеспечить непросто, поскольку выборка обычно объединяет объекты, относящиеся к одному семейству, у которых имеет место закономерное изменение многих факторов от объекта к объекту.

Качество регрессионных моделей, как правило, проверяют с использованием следующих статистических показателей.

Стандартное отклонение ошибки уравнения регрессии (ошибка оценки):

где п - объем выборки (количество аналогов);

к - количество факторов (факторов стоимости);

Ошибка, необъясняемая регрессионным уравнением (рис. 3.2);

у. - фактическое значение результирующей переменной (например, стоимости); y t - расчетное значение результирующей переменной.

Этот показатель также называют стандартной ошибкой оценки {СКО ошибки ). На рисунке точками обозначены конкретные значения выборки, символом обозначена линия среднего значений выборки, наклонная штрихпунктирная линия - это линия регрессии.

Рис. 3.2.

Стандартное отклонение ошибки оценки измеряет величину отклонения фактических значений у от соответствующих расчетных значений у { , полученных с помощью регрессионной модели. Если выборка, на которой построена модель, подчинена нормальному закону распределения, то можно утверждать, что 68% реальных значений у находятся в диапазоне у ± & е от линии регрессии, а 95% - в диапазоне у ± 2d e . Этот показатель удобен тем, что единицы измерения сг? совпадают с единицами измерения у ,. В этой связи его можно использовать для указания точности получаемого в процессе оценки результата. Например, в сертификате стоимости можно указать, что полученное с использованием регрессионной модели значение рыночной стоимости V с вероятностью 95% находится в диапазоне от (V -2d,.) до (у + 2d s).

Коэффициент вариации результирующей переменной:

где у - среднее значение результирующей переменной (рис. 3.2).

В регрессионном анализе коэффициент вариации var представляет собой стандартное отклонение результата, выраженное в виде процентного отношения к среднему значению результирующей переменной. Коэффициент вариации может служить критерием прогнозных качеств полученной регрессионной модели: чем меньше величина var , тем более высокими являются прогнозные качества модели. Использование коэффициента вариации предпочтительнее показателя & е, так как он является относительным показателем. При практическом использовании данного показателя можно порекомендовать не применять модель, коэффициент вариации которой превышает 33%, так как в этом случае нельзя говорить о том, что данные выборки подчинены нормальному закону распределения.

Коэффициент детерминации (квадрат коэффициента множественной корреляции):

Данный показатель используется для анализа общего качества полученной регрессионной модели. Он указывает, какой процент вариации результирующей переменной объясняется влиянием всех включенных в модель факторных переменных. Коэффициент детерминации всегда лежит в интервале от нуля до единицы. Чем ближе значение коэффициента детерминации к единице, тем лучше модель описывает исходный ряд данных. Коэффициент детерминации можно представить иначе:

Здесь- ошибка, объясняемая регрессионной моделью,

а - ошибка, необъясняемая

регрессионной моделью. С экономической точки зрения данный критерий позволяет судить о том, какой процент вариации цен объясняется регрессионным уравнением.

Точную границу приемлемости показателя R 2 для всех случаев указать невозможно. Нужно принимать во внимание и объем выборки, и содержательную интерпретацию уравнения. Как правило, при исследовании данных об однотипных объектах, полученных примерно в один и тот же момент времени величина R 2 не превышает уровня 0,6-0,7. Если все ошибки прогнозирования равны нулю, т.е. когда связь между результирующей и факторными переменными является функциональной, то R 2 =1.

Скорректированный коэффициент детерминации:

Необходимость введения скорректированного коэффициента детерминации объясняется тем, что при увеличении числа факторов к обычный коэффициент детерминации практически всегда увеличивается, но уменьшается число степеней свободы (п - к - 1). Введенная корректировка всегда уменьшает значение R 2 , поскольку (п - 1) > {п- к - 1). В результате величина R 2 CKOf) даже может стать отрицательной. Это означает, что величина R 2 была близка к нулю до корректировки и объясняемая с помощью уравнения регрессии доля дисперсии переменной у очень мала.

Из двух вариантов регрессионных моделей, которые различаются величиной скорректированного коэффициента детерминации, но имеют одинаково хорошие другие критерии качества, предпочтительнее вариант с большим значением скорректированного коэффициента детерминации. Корректировка коэффициента детерминации не производится, если (п - к): к> 20.

Коэффициент Фишера:

Данный критерий используется для оценки значимости коэффициента детерминации. Остаточная сумма квадратов представляет собой показатель ошибки предсказания с помощью регрессии известных значений стоимости у.. Ее сравнение с регрессионной суммой квадратов показывает, во сколько раз регрессионная зависимость предсказывает результат лучше, чем среднее у . Существует таблица критических значений F R коэффициента Фишера, зависящих от числа степеней свободы числителя - к , знаменателя v 2 = п - к - 1 и уровня значимости а. Если вычисленное значение критерия Фишера F R больше табличного значения, то гипотеза о незначимости коэффициента детерминации, т.е. о несоответствии заложенных в уравнении регрессии связей реально существующим, с вероятностью р = 1 - а отвергается.

Средняя ошибка аппроксимации (среднее процентное отклонение) вычисляется как средняя относительная разность, выраженная в процентах, между фактическими и расчетными значениями результирующей переменной:

Чем меньше значение данного показателя, тем лучше прогнозные качества модели. При значении данного показателя не выше 7% говорят о высокой точности модели. Если 8 > 15%, говорят о неудовлетворительной точности модели.

Стандартная ошибка коэффициента регрессии:

где (/I) -1 .- диагональный элемент матрицы {Х Г Х)~ 1 к - количество факторов;

X - матрица значений факторных переменных:

X 7 - транспонированная матрица значений факторных переменных;

(ЖЛ) _| - матрица, обратная матрице.

Чем меньше эти показатели для каждого коэффициента регрессии, тем надежнее оценка соответствующего коэффициента регрессии.

Критерий Стьюдента (t-статистика):

Этот критерий позволяет измерить степень надежности (существенности) связи, обусловленной данным коэффициентом регрессии. Если вычисленное значение t . больше табличного значения

t av , где v - п - к - 1 - число степеней свободы, то гипотеза о том, что данный коэффициент является статистически незначимым, отвергается с вероятностью (100 - а)%. Существуют специальные таблицы /-распределения, позволяющие по заданному уровню значимости а и числу степеней свободы v определять критическое значение критерия. Наиболее часто употребляемое значение а равно 5%.

Мультиколлинеарность , т.е. эффект взаимных связей между факторными переменными, приводит к необходимости довольствоваться ограниченным их числом. Если это не учесть, то можно в итоге получить нелогичную регрессионную модель. Чтобы избежать негативного эффекта мультиколлинеарности, до построения множественной регрессионной модели рассчитываются коэффициенты парной корреляции r xjxj между отобранными переменными х. и х

Здесь XjX; - среднее значение произведения двух факторных переменных;

XjXj - произведение средних значений двух факторных переменных;

Оценка дисперсии факторной переменной х..

Считается, что две переменные регрессионно связаны между собой (т.е. коллинеарные), если коэффициент их парной корреляции по абсолютной величине строго больше 0,8. В этом случае какую-либо из этих переменных надо исключить из рассмотрения.

С целью расширения возможностей экономического анализа получаемых регрессионных моделей используются средние коэффициенты эластичности, определяемые по формуле:

где Xj - среднее значение соответствующей факторной переменной;

у - среднее значение результирующей переменной; a i - коэффициент регрессии при соответствующей факторной переменной.

Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результирующей переменной при изменении факторной переменной на 1 %, т.е. как реагирует результирующая переменная на изменение факторной переменной. Например, как реагирует цена кв. м площади квартиры на удаление от центра города.

Полезным с точки зрения анализа значимости того или иного коэффициента регрессии является оценка частного коэффициента детерминации:

Здесь - оценка дисперсии результирующей

переменной. Данный коэффициент показывает, на сколько процентов вариация результирующей переменной объясняется вариацией /-й факторной переменной, входящей в уравнение регрессии.

• Под гедонистическими характеристиками понимаются характеристики объекта, отражающие его полезные (ценные) с точки зрения покупателей и продавцов свойства.

После того как с помощью корреляционного анализа выявлено наличие статистических связей между переменными и оценена степень их тесноты, обычно переходят к математическому описанию конкретного вида зависимостей с использованием регрессионного анализа. С этой целью подбирают класс функций, связывающий результативный показатель у и аргументы х 1, х 2,…, х к отбирают наиболее информативные аргументы, вычисляют оценки неизвестных значений параметров уравнения связи и анализируют свойства полученного уравнения.

Функция f(х 1, х 2,…, х к) описывающая зависимость среднего значения результативного признака у от заданных значений аргументов, называется функцией (уравнением) регрессии. Термин «регрессия» (лат. -regression- отступление, возврат к чему-либо) введен английским психологом и антропологом Ф.Гальтоном и связан исключительно со спецификой одного из первых конкретных примеров, в котором это понятие было использовано. Так, обрабатывая статистические данные в связи с анализом наследственности роста, Ф. Гальтон нашел, что если отцы отклоняются от среднего роста всех отцов на x дюймов, то их сыновья отклоняются от среднего роста всех сыновей меньше, чем на x дюймов. Выявленная тенденция была названа «регрессией к среднему состоянию». С тех пор термин «регрессия» широко используется в статистической литературе, хотя во многих случаях он недостаточно точно характеризует понятие статистической зависимости.

Для точного описания уравнения регрессии необходимо знать закон распределения результативного показателя у. В статистической практике обычно приходится ограничиваться поиском подходящих аппроксимаций для неизвестной истинной функции регрессии, так как исследователь не располагает точным знанем условного закона распределения вероятностей анализируемого результатирующего показателя у при заданных значениях аргумента х.

Рассмотрим взаимоотношение между истинной f(х) = М(у1х), мо дельной регрессией? и оценкой y регрессии. Пусть результативный показатель у связан с аргументом х соотношением:

где - е случайная величина, имеющая нормальный закон распределения, причем Ме = 0 и D е = у 2 . Истинная функция регрессии в этом случае имеет вид: f (х) = М(у/х) = 2х 1.5 .

Предположим, что точный вид истинного уравнения регрессии нам не известен, но мы располагаем девятью наблюдениями над двумерной случайной величиной, связанной соотношением уi= 2х1,5+е, и представленной на рис. 1

Рисунок 1 - Взаимное расположение истиной f (х) и теоретической? модели регрессии

Расположение точек на рис. 1 позволяет ограничиться классом линейных зависимостей вида? = в 0 +в 1 x. С помощью метода наименьших квадратов найдем оценку уравнения регрессии у = b 0 +b 1 x. Для сравнения на рис. 1 приводятся графики истинной функции регрессии у=2х 1,5 , теоретической аппроксимирующей функции регрессии? = в 0 +в 1 x .

Поскольку мы ошиблись в выборе класса функции регрессии, а это достаточно часто встречается в практике статистических исследований, то наши статистические выводы и оценки окажутся ошибочными. И как бы мы ни увеличивали объем наблюдений, наша выборочная оценка у не будет близка к истинной функции регрессии f (х). Если бы мы правильно выбрали класс функций регрессии, то неточность в описании f(х) с помощью? объяснялась бы только ограниченностью выборки.

С целью наилучшего восстановления по исходным статистическим данным условного значения результативного показателя у(х) и неизвестной функции регрессии f(х) = М(у/х) наиболее часто используют следующие критерии адекватности (функции потерь).

Метод наименьших квадратов. Согласно ему минимизируется квадрат отклонения наблюдаемых значений результативного показателя у, (i = 1,2,..., п) от модельных значений,? = f(х i), где, х i - значение вектора аргументов в i-м наблюдении: ?(y i - f(х i) 2 > min. Получаемая регрессия называется среднеквадратической.

Метод наименьших модулей. Согласно ему минимизируется сумма абсолютных отклонений наблюдаемых значений результативного показателя от модульных значений. И получаем,? = f(х i), среднеабсолютную медианную регрессию? |y i - f(х i)| >min.

Регрессионным анализом называется метод статистического анализа зависимости случайной величины у от переменных х j = (j=1,2,..., к), рассматриваемых в регрессионном анализе как неслучайные величины, независимо от истинного закона распределения х j.

Обычно предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием у, являющимся функцией от аргументов х/ (/= 1, 2,..., к) и постоянной, не зависящей от аргументов, дисперсией у 2 .

В общем линейная модель регрессионного анализа имеет вид:

Y = Уk j=0 вj цj (x1 , x2 . . .. ,xk )+Э

где ц j - некоторая функция его переменных - x 1 , x 2 . . .. ,x k , Э - случайная величина с нулевым математическим ожиданием и дисперсией у 2 .

В регрессионном анализе вид уравнения регрессии выбирают исходя из физической сущности изучаемого явления и результатов наблюдения.

Оценки неизвестных параметров уравнения регрессии находят обычно методом наименьших квадратов. Ниже остановимся более подробно на этой проблеме.

Двумерное линейное уравнение регрессии. Пусть на основании анализа исследуемого явления предполагается, что в «среднем» у есть линейная функция от х, т. е. имеется уравнение регрессии

у=М(у/х)=в 0 + в 1 х)

где М(у1х) - условное математическое ожидание случайной величины у при заданном х; в 0 и в 1 - неизвестные параметры генеральной совокупности, которые надлежит оценить по результатам выборочных наблюдений.

Предположим, что для оценки параметров в 0 и в 1 из двухмерной генеральной совокупности (х, у) взята выборка объемом n, где (х, у,) результат i-го наблюдения (i = 1, 2,..., n). В этом случае модель регрессионного анализа имеет вид:

y j = в 0 + в 1 x+е j .

где е j .- независимые нормально распределенные случайные величины с нулевым математическим ожиданием и дисперсией у 2 , т. е. М е j . = 0;

D е j .= у 2 для всех i = 1, 2,..., n.

Согласно методу наименьших квадратов в качестве оценок неизвестных параметров в 0 и в 1 следует брать такие значения выборочных характеристик b 0 и b 1 , которые минимизируют сумму квадратов отклонений значений результативного признака у i от условного математического ожидания? i

Методику определения влияния характеристик маркетинга на прибыль предприятия рассмотрим на примере семнадцати типичных предприятий, имеющих средние размеры и показатели хозяйственной деятельности.

При решении задачи учитывались следующие характеристики, выявленные в результате анкетного опроса как наиболее значимые (важные):

* инновационная деятельность предприятия;

* планирование ассортимента производимой продукции;

* формирование ценовой политики;

* взаимоотношения с общественностью;

* система сбыта;

* система стимулирования работников.

На основе системы сравнений по факторам были построены квадратные матрицы смежности, в которых вычислялись значения относительных приоритетов по каждому фактору: инновационная деятельность предприятия, планирование ассортимента производимой продукции, формирование ценовой политики, реклама, взаимоотношения с общественностью, система сбыта, система стимулирования работников.

Оценки приоритетов по фактору «взаимоотношения с общественностью» получены в результате анкетирования специалистов предприятия. Приняты следующие обозначения: > (лучше), > (лучше или одинаково), = (одинаково), < (хуже или одинаково), <

Далее решалась задача комплексной оценки уровня маркетинга предприятия. При расчете показателя была определена значимость (вес) рассмотренных частных признаков и решалась задача линейного свертывания частных показателей. Обработка данных производилась по специально разработанным программам.

Далее рассчитывается комплексная оценка уровня маркетинга предприятия -- коэффициент маркетинга, который вносится в таблице 1. Кроме того, в названую таблицу включены показатели, характеризующие предприятие в целом. Данные в таблице будут использованы для проведения регрессионного анализа. Результативным признаком является прибыль. В качестве факторных признаков наряду с коэффициентом маркетинга использованы следующие показатели: объем валовой продукции, стоимость основных фондов, численность работников, коэффициент специализации.

Таблица 1 - Исходные данные для регрессионного анализа

По данным таблицы и на основе факторов с наиболее существенными значениями коэффициентов корреляции были построены регрессионные функции зависимости прибыли от факторов.

Уравнение регрессии в нашем случае примет вид:

О количественном влиянии рассмотренных выше факторов на величину прибыли говорят коэффициенты уравнения регрессии. Они показывают, на сколько тысяч рублей изменяется ее величина при изменении факторного признака на одну единицу. Как следует из уравнения, увеличение коэффициента комплекса маркетинга на одну единицу дает прирост прибыли на 1547,7 тыс. руб. Это говорит о том, что в совершенствовании маркетинговой деятельности кроется огромный потенциал улучшения экономических показателей предприятий.

При исследовании эффективности маркетинга наиболее интересным и самым важным факторным признаком является фактор Х5 -- коэффициент маркетинга. В соответствии с теорией статистики достоинство имеющегося уравнения множественной регрессии является возможность оценивать изолированное влияние каждого фактора, в том числе фактора маркетинга.

Результаты проведенного регрессионного анализа имеют и более широкое применение, чем для расчета параметров уравнения. Критерий отнесения (КЭф,) предприятий к относительно лучшим или относительно худшим основан на относительном показателе результата:

где Y фактi - фактическая величина i-го предприятия, тыс. руб.;

Y расчi -величина прибыли i-го предприятия, полученная расчетным путем по уравнению регрессии

В терминах решаемой задачи величина носит название «коэффициент эффективности». Деятельность предприятия можно признать эффективной в тех случаях, когда величина коэффициента больше единицы. Это означает, что фактическая прибыль больше прибыли, усредненной по выборке.

Фактические и расчетные значения прибыли представлены в табл. 2.

Таблица 2 - Анализ результативного признака в регрессионной модели

Анализ таблицы показывает, что в нашем случае деятельность предприятий 3, 5, 7, 9, 12, 14, 15, 17 за рассматриваемый период можно признать успешной.

Основная цель регрессионного анализа состоит в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения.
Задачи регрессионного анализа :
а) Установление формы зависимости. Относительно характера и формы зависимости между явлениями, различают положительную линейную и нелинейную и отрицательную линейную и нелинейную регрессию.
б) Определение функции регрессии в виде математического уравнения того или иного типа и установление влияния объясняющих переменных на зависимую переменную.
в) Оценка неизвестных значений зависимой переменной. С помощью функции регрессии можно воспроизвести значения зависимой переменной внутри интервала заданных значений объясняющих переменных (т. е. решить задачу интерполяции) или оценить течение процесса вне заданного интервала (т. е. решить задачу экстраполяции). Результат представляет собой оценку значения зависимой переменной.

Парная регрессия - уравнение связи двух переменных у и х: , где y - зависимая переменная (результативный признак); x - независимая, объясняющая переменная (признак-фактор).

Различают линейные и нелинейные регрессии.
Линейная регрессия: y = a + bx + ε
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:

Регрессии, нелинейные по оцениваемым параметрам: Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, Используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, т.е.
.
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b:

Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии :

и индекс корреляции - для нелинейной регрессии:

Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации .
Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
.
Допустимый предел значений - не более 8-10%.
Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
.

Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
,
где - общая сумма квадратов отклонений;
- сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
- остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R 2:

Коэффициент детерминации - квадрат коэффициента или индекса корреляции.

F-тест - оценивание качества уравнения регрессии - состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F факт и критического (табличного) F табл значений F-критерия Фишера. F факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
,
где n - число единиц совокупности; m - число параметров при переменных х.
F табл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.
Если F табл < F факт, то Н о - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F табл > F факт, то гипотеза Н о не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н о о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
; ; .
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:



Сравнивая фактическое и критическое (табличное) значения t-статистики - t табл и t факт - принимаем или отвергаем гипотезу Н о.
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством

Если t табл < t факт то H o отклоняется, т.е. a, b и не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t табл > t факт то гипотеза Н о не отклоняется и признается случайная природа формирования а, b или .
Для расчета доверительного интервала определяем предельную ошибку D для каждого показателя:
, .
Формулы для расчета доверительных интервалов имеют следующий вид:
; ;
; ;
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения . Вычисляется средняя стандартная ошибка прогноза :
,
где
и строится доверительный интервал прогноза:
; ;
где .

Пример решения

Задача №1 . По семи территориям Уральского района За 199Х г. известны значения двух признаков.
Таблица 1.
Требуется: 1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной (предварительно нужно произвести процедуру линеаризации переменных, путем логарифмирования обеих частей);
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации и F-критерий Фишера.

Решение (Вариант №1)

Для расчета параметров a и b линейной регрессии (расчет можно проводить с помощью калькулятора).
решаем систему нормальных уравнений относительно а и b:
По исходным данным рассчитываем :

	y	x	yx	x 2	y 2			A i
l	68,8	45,1	3102,88	2034,01	4733,44	61,3	7,5	10,9
2	61,2	59,0	3610,80	3481,00	3745,44	56,5	4,7	7,7
3	59,9	57,2	3426,28	3271,84	3588,01	57,1	2,8	4,7
4	56,7	61,8	3504,06	3819,24	3214,89	55,5	1,2	2,1
5	55,0	58,8	3234,00	3457,44	3025,00	56,5	-1,5	2,7
6	54,3	47,2	2562,96	2227,84	2948,49	60,5	-6,2	11,4
7	49,3	55,2	2721,36	3047,04	2430,49	57,8	-8,5	17,2
Итого	405,2	384,3	22162,34	21338,41	23685,76	405,2	0,0	56,7
Ср. знач. (Итого/n)	57,89	54,90	3166,05	3048,34	3383,68	X	X	8,1
s	5,74	5,86	X	X	X	X	X	X
s 2	32,92	34,34	X	X	X	X	X	X

Уравнение регрессии: у = 76,88 - 0,35х. С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ных пункта.
Рассчитаем линейный коэффициент парной корреляции:

Связь умеренная, обратная.
Определим коэффициент детерминации:

Вариация результата на 12,7% объясняется вариацией фактора х. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения . Найдем величину средней ошибки аппроксимации :

В среднем расчетные значения отклоняются от фактических на 8,1%.
Рассчитаем F-критерий:

поскольку 1< F < ¥ , следует рассмотреть F -1 .
Полученное значение указывает на необходимость принять гипотезу Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
1б. Построению степенной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:


где Y=lg(y), X=lg(x), C=lg(a).

Для расчетов используем данные табл. 1.3.

Таблица 1.3

	Y	X	YX	Y 2	X 2				A i
1	1,8376	1,6542	3,0398	3,3768	2,7364	61,0	7,8	60,8	11,3
2	1,7868	1,7709	3,1642	3,1927	3,1361	56,3	4,9	24,0	8,0
3	1,7774	1,7574	3,1236	3,1592	3,0885	56,8	3,1	9,6	5,2
4	1,7536	1,7910	3,1407	3,0751	3,2077	55,5	1,2	1,4	2,1
5	1,7404	1,7694	3,0795	3,0290	3,1308	56,3	-1,3	1,7	2,4
6	1,7348	1,6739	2,9039	3,0095	2,8019	60,2	-5,9	34,8	10,9
7	1,6928	1,7419	2,9487	2,8656	3,0342	57,4	-8,1	65,6	16,4
Итого	12,3234	12,1587	21,4003	21,7078	21,1355	403,5	1,7	197,9	56,3
Среднее значение	1,7605	1,7370	3,0572	3,1011	3,0194	X	X	28,27	8,0
σ	0,0425	0,0484	X	X	X	X	X	X	X
σ 2	0,0018	0,0023	X	X	X	X	X	X	X

Рассчитаем С иb:


Получим линейное уравнение:.
Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата. По ним рассчитаем показатели: тесноты связи - индекс корреляции и среднюю ошибку аппроксимации

Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь.

1в . Построению уравнения показательной кривой

предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:

Для расчетов используем данные таблицы.

	Y	x	Yx	Y 2	x 2				A i
1	1,8376	45,1	82,8758	3,3768	2034,01	60,7	8,1	65,61	11,8
2	1,7868	59,0	105,4212	3,1927	3481,00	56,4	4,8	23,04	7,8
3	1,7774	57,2	101,6673	3,1592	3271,84	56,9	3,0	9,00	5,0
4	1,7536	61,8	108,3725	3,0751	3819,24	55,5	1,2	1,44	2,1
5	1,7404	58,8	102,3355	3,0290	3457,44	56,4	-1,4	1,96	2,5
6	1,7348	47,2	81,8826	3,0095	2227,84	60,0	-5,7	32,49	10,5
7	1,6928	55,2	93,4426	2,8656	3047,04	57,5	-8,2	67,24	16,6
Итого	12,3234	384,3	675,9974	21,7078	21338,41	403,4	-1,8	200,78	56,3
Ср. зн.	1,7605	54,9	96,5711	3,1011	3048,34	X	X	28,68	8,0
σ	0,0425	5,86	X	X	X	X	X	X	X
σ 2	0,0018	34,339	X	X	X	X	X	X	X

Значения параметров регрессии A и В составили:


Получено линейное уравнение: . Произведем потенцирование полученного уравнения и запишем его в обычной форме:

Тесноту связи оценим через индекс корреляции :

Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.

Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.

Регрессионный анализ в Excel

Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.

Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.

Регрессия бывает:

• линейной (у = а + bx);
• параболической (y = a + bx + cx 2);
• экспоненциальной (y = a * exp(bx));
• степенной (y = a*x^b);
• гиперболической (y = b/x + a);
• логарифмической (y = b * 1n(x) + a);
• показательной (y = a * b^x).

Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.

Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:

У = а 0 + а 1 х 1 +…+а к х к.

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).

В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».

Активируем мощный аналитический инструмент:

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

В первую очередь обращаем внимание на R-квадрат и коэффициенты.

R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».

Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.

Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.



Корреляционный анализ в Excel

Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.

Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.

Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.

Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.

Для нахождения парных коэффициентов применяется функция КОРРЕЛ.

Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.

Ставим курсор в любую ячейку и нажимаем кнопку fx.

1. В категории «Статистические» выбираем функцию КОРРЕЛ.
2. Аргумент «Массив 1» - первый диапазон значений – время работы станка: А2:А14.
3. Аргумент «Массив 2» - второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.

Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).

Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.

Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:

Корреляционно-регрессионный анализ

На практике эти две методики часто применяются вместе.

Пример:

Теперь стали видны и данные регрессионного анализа.

ВЫВОД ИТОГОВ

Таблица 8.3а. Регрессионная статистика

Регрессионная статистика
Множественный R	0,998364
R-квадрат	0,99673
Нормированный R-квадрат	0,996321
Стандартная ошибка	0,42405
Наблюдения	10

Сначала рассмотрим верхнюю часть расчетов, представленную в таблице 8.3а , - регрессионную статистику.

Величина R-квадрат , называемая также мерой определенности, характеризует качество полученной регрессионной прямой. Это качество выражается степенью соответствия между исходными данными и регрессионной моделью (расчетными данными). Мера определенности всегда находится в пределах интервала .

В большинстве случаев значение R-квадрат находится между этими значениями, называемыми экстремальными, т.е. между нулем и единицей.

Если значение R-квадрата близко к единице, это означает, что построенная модель объясняет почти всю изменчивость соответствующих переменных. И наоборот, значение R-квадрата , близкое к нулю, означает плохое качество построенной модели.

В нашем примере мера определенности равна 0,99673, что говорит об очень хорошей подгонке регрессионной прямой к исходным данным.

Множественный R - коэффициент множественной корреляции R - выражает степень зависимости независимых переменных (X) и зависимой переменной (Y).

Множественный R равен квадратному корню из коэффициента детерминации, эта величина принимает значения в интервале от нуля до единицы.

В простом линейном регрессионном анализе множественный R равен коэффициенту корреляции Пирсона. Действительно, множественный R в нашем случае равен коэффициенту корреляции Пирсона из предыдущего примера (0,998364).

Таблица 8.3б. Коэффициенты регрессии

	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	2,694545455	0,33176878	8,121757129
Переменная X 1	2,305454545	0,04668634	49,38177965
* Приведен усеченный вариант расчетов

Теперь рассмотрим среднюю часть расчетов, представленную в таблице 8.3б . Здесь даны коэффициент регрессии b (2,305454545) и смещение по оси ординат, т.е. константа a (2,694545455).

Исходя из расчетов, можем записать уравнение регрессии таким образом:

Y= x*2,305454545+2,694545455

Направление связи между переменными определяется на основании знаков (отрицательный или положительный) коэффициентов регрессии (коэффициента b).

Если знак при коэффициенте регрессии - положительный, связь зависимой переменной с независимой будет положительной. В нашем случае знак коэффициента регрессии положительный, следовательно, связь также является положительной.

Если знак при коэффициенте регрессии - отрицательный, связь зависимой переменной с независимой является отрицательной (обратной).

В таблице 8.3в . представлены результаты вывода остатков . Для того чтобы эти результаты появились в отчете, необходимо при запуске инструмента "Регрессия" активировать чекбокс "Остатки".

ВЫВОД ОСТАТКА

Таблица 8.3в. Остатки

Наблюдение	Предсказанное Y	Остатки	Стандартные остатки
1	9,610909091	-0,610909091	-1,528044662
2	7,305454545	-0,305454545	-0,764022331
3	11,91636364	0,083636364	0,209196591
4	14,22181818	0,778181818	1,946437843
5	16,52727273	0,472727273	1,182415512
6	18,83272727	0,167272727	0,418393181
7	21,13818182	-0,138181818	-0,34562915
8	23,44363636	-0,043636364	-0,109146047
9	25,74909091	-0,149090909	-0,372915662
10	28,05454545	-0,254545455	-0,636685276

При помощи этой части отчета мы можем видеть отклонения каждой точки от построенной линии регрессии. Наибольшее абсолютное значение

---