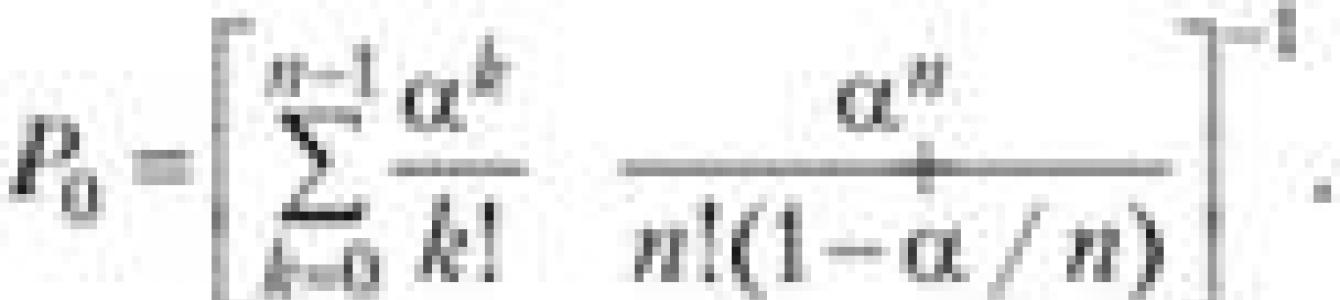Многие экономические задачи связаны с системами массового обслуживания (СМО), т.е. такими системами, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо услуг, с другой – происходит удовлетворение этих запросов. СМО включает в себя следующие элементы: источник требований, входящий поток требований, очередь, обслуживающие устройства (каналы обслуживания), выходящий поток требований. Исследованием таких систем занимается теория массового обслуживания.
Методами теории массового обслуживания могут быть решены многие задачи исследования процессов, происходящих в экономике. Так, в организации торговли эти методы позволяют определить оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и другие параметры. Другим характерным примером систем массового обслуживания могут служить склады или базы снабженческо-сбытовых организаций, и задача теории массового обслуживания в данном случае сводится к тому, чтобы установить оптимальное соотношение между числом поступающих на базу требований на обслуживание и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы минимальными. Теория массового обслуживания может найти применение и при расчете площади складских помещений, при этом складская площадь рассматривается как обслуживающее устройство, а прибытие транспортных средств под выгрузку – как требование. Модели теории массового обслуживания применяются также при решении ряда задач организации и нормирования труда, других социально-экономических проблем.
Системы массового обслуживания могут быть классифицированы по ряду признаков.
- 1. В зависимости от условий ожидания
начала обслуживания различают:
- – СМО с потерями (отказами);
- – СМО с ожиданием.
В СМО с отказами требования, поступающие в момент, когда все каналы обслуживания заняты, получают отказ и теряются. Классическим примером системы с отказами является телефонная станция. Если вызываемый абонент занят, то требование па соединение с ним получает отказ и теряется.
В СМО с ожиданием требование, застав все обслуживающие каналы занятыми, становится в очередь и ожидает, пока не освободится один из обслуживающих каналов.
СМО, допускающие очередь, но с ограниченным числом требований в ней, называются системами с ограниченной длиной очереди.
СМО, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания.
- 2. По числу каналов обслуживания
СМО делятся на:
- – одноканальные ,
- – многоканальные.
- 3. По месту нахождения источника требований СМО делятся на:
- – разомкнутые, когда источник требования находится вне системы;
- – замкнутые, когда источник находится в самой системе.
Примером разомкнутой системы может служить ателье по ремонту телевизоров. Здесь неисправные телевизоры – это источник требований на их обслуживание, находятся вне самой системы, число требований можно считать неограниченным. К замкнутым СМО относится, например, станочный участок, в котором станки являются источником неисправностей, а следовательно, источником требований на их обслуживание, например, бригадой наладчиков.
Возможны и другие признаки классификации СМО, например по дисциплине обслуживания, однофазные и многофазные СМО и др.
Методы и модели, применяющиеся в теории массового обслуживания, можно условно разделить на аналитические и имитационные.
Аналитические методы теории массового обслуживания позволяют получить характеристики системы как некоторые функции параметров ее функционирования. Благодаря этому появляется возможность проводить качественный анализ влияния отдельных факторов на эффективность работы СМО. Имитационные методы основаны на моделировании процессов массового обслуживания на ЭВМ и применяются, если невозможно применение аналитических моделей; ряд основных понятий имитационного моделирования рассмотрен в параграфе 3.5. Далее будем рассматривать аналитические методы моделирования СМО.
В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач массового обслуживания, в которых входящий поток требований является простейшим (пуассоновским ).
Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, т.е. вероятность поступления за время t ровно k требований задается формулой
Простейший поток обладает тремя основными свойствами: ординарности, стационарности и отсутствием последействия.
Ординарность потока означает практическую невозможность одновременного поступления двух и более требований. Например, достаточно малой является вероятность того, что из группы станков, обслуживаемых бригадой ремонтников, одновременно выйдут из строя сразу несколько станков.
Стационарным называется поток, для которого математическое ожидание числа требований, поступающих в систему в единицу времени (обозначим λ), не меняется во времени. Таким образом, вероятность поступления в систему определенного количества требований в течение заданного промежутка времени Δί зависит от его величины и не зависит от начала его отсчета на оси времени.
Отсутствие последействия означает, что число требований, поступивших в систему до момента ί, не определяет того, сколько требований поступит в систему за промежуток времени от t до t + Δt .
Например, если на ткацком станке в данный момент произошел обрыв нити и он устранен ткачихой, то это не определяет, произойдет новый обрыв на данном станке в следующий момент или нет, тем более это не влияет на вероятность возникновения обрыва на других станках.
Важная характеристика СМО – время обслуживания требований в системе. Время обслуживания одного требования является, как правило, случайной величиной и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории и особенно в практических приложениях получил экспоненциальный закон распределения времени обслуживания. Функция распределения для этого закона имеет вид
т.е. вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой (8.44), где μ – параметр экспоненциального закона распределения времени обслуживания требований в системе, т.е. величина, обратная среднему времени обслуживания :
Рассмотрим аналитические модели наиболее распространенных СМО с ожиданием, т.е. таких СМО, в которых требования, поступившие в момент, когда все обслуживающие каналы заняты, ставятся в очередь и обслуживаются по мере освобождения каналов.
Общая постановка задачи состоит в следующем. Система имеет п обслуживающих каналов, каждый из которых может одновременно обслуживать только одно требование.
В систему поступает простейший (пуассоновский) поток требований с параметром λ. Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше п требований (т.е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания.
Время обслуживания каждого требования t об – случайная величина, которая подчиняется экспоненциальному закону распределения с параметром μ.
СМО с ожиданием можно разбить на две большие группы: замкнутые и разомкнутые. К замкнутым относятся системы, в которых поступающий поток требований возникает в самой системе и ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится потенциальным источником требований на накладку. В подобных системах общее число циркулирующих требований конечно и чаще всего постоянно.
Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, портов и др. Для этих систем поступающий поток требований можно считать неограниченным.
Отмеченные особенности функционирования систем этих двух видов накладывают определенные условия на используемый математический аппарат. Расчет характеристик работы СМО различного вида может быть проведен на основе расчета вероятностей состояний СМО (так называемые формулы Эрланга ).
Рассмотрим алгоритмы расчета показателей качества функционирования разомкнутой системы массового обслуживания с ожиданием.
При изучении таких систем рассчитывают различные показатели эффективности обслуживающей системы. В качестве основных показателей могут быть вероятность того, что все каналы свободны или заняты, математическое ожидание длины очереди (средняя длина очереди), коэффициенты занятости и простоя каналов обслуживания и др.
- 1. Введем в рассмотрение параметр α = λ/μ. Заметим, что если 007 /п
- 1. Вероятность того, что все каналы свободны от обслуживания:
![]() (8.46)
(8.46)
2. Вероятность того, что занято ровно k обслуживающих каналов при условии, что общее число требований, находящихся на обслуживании, не превосходит числа обслуживающих каналов:
к требований в случае, когда их число больше числа обслуживающих каналов:
4. Вероятность того, что все обслуживающие каналы заняты:
![]() (8.49)
(8.49)
5. Среднее время ожидания требованием начала обслуживания в системе:
![]() (8.50)
(8.50)
6. Средняя длина очереди:
7. Среднее число свободных от обслуживания каналов:
![]() (8.52)
(8.52)
8. Коэффициент простоя каналов:
9. Среднее число занятых обслуживанием каналов:
10. Коэффициент загрузки каналов:
Пример 8.6. Пусть филиал фирмы по ремонту радиоаппаратуры имеет п = 5 опытных мастеров. В среднем в течение рабочего дня от населения поступает в ремонт λ = 10 радиоаппаратов. Общее число радиоаппаратов, находящихся в эксплуатации у населения, очень велико, и они независимо друг от друга в различное время выходят из строя. Поэтому есть все основания полагать, что поток заявок на ремонт аппаратуры является случайным, пуассоновским. В свою очередь каждый аппарат в зависимости от характера неисправности также требует различного случайного времени на ремонт. Время на проведение ремонта зависит во многом от серьезности полученного повреждения, квалификации мастера и множества других причин. Пусть статистика показала, что время ремонта подчиняется экспоненциальному закону; при этом в среднем в течение рабочего дня каждый из мастеров успевает отремонтировать μ = 2,5 радиоаппарата. Требуется оценить работу филиала фирмы по ремонту радиоаппаратуры, рассчитав ряд основных характеристик данной СМО.
За единицу времени принимаем 1 рабочий день (7 часов).
1. Определим параметр:
![]()
так как α < п, то очередь не может расти безгранично.
2. Вероятность того, что все мастера свободны от ремонта аппаратуры, равна согласно (8.46):
3. Вероятность того, что все мастера заняты ремонтом, находим по (8.49): ![]()
Это означает, что 55,4% времени мастера полностью загружены работой.
4. Среднее время обслуживания (ремонта) одного аппарата согласно (8.45):
- (при условии семичасового рабочего дня).
- 5. В среднем время ожидания каждого неисправного аппарата начала ремонта равно по (8.50):
![]()
6. Очень важной характеристикой является средняя длина очереди, которая определяет необходимое место для хранения аппаратуры, требующей ремонта; находим ее по (8.51):
![]()
7. Определим среднее число мастеров, свободных от работы, по (8.52):
Таким образом, в среднем в течение рабочего дня ремонтом заняты четыре мастера из пяти.
Перейдем к рассмотрению алгоритмов расчета характеристик функционирования замкнутых СМО. Поскольку система замкнутая, то к постановке задачи следует добавить условие: поток поступающих требований ограничен, т.е. в системе обслуживания одновременно не может находиться больше т требований (т – число обслуживаемых объектов).
За критерий, характеризующий качество функционирования рассматриваемой системы, выберем отношение средней длины очереди к наибольшему числу требований, находящихся одновременно в обслуживающей системе, – коэффициент простоя обслуживаемого объекта. В качестве другого критерия возьмем отношение среднего числа незанятых обслуживающих каналов к их общему числу – коэффициент простоя обслуживающего канала.
Первый из названных критериев характеризует потери времени из-за ожидания начала обслуживания; второй показывает полноту загрузки обслуживающей системы.
Очевидно, что очередь может возникнуть, лишь когда число каналов меньше наибольшего числа требований, находящихся одновременно в обслуживающей системе (п < т ).
Приведем последовательность расчетов характеристик замкнутых СМО и необходимые формулы.
![]() (8.56)
(8.56)
3. Вероятность того, что в системе находится к требований для случая, когда их число больше числа обслуживающих каналов:
![]() (8.57)
(8.57)
4. Вероятность того, что все обслуживающие каналы свободны, определим, используя очевидное условие:
Величину можно получить также путем подстановки в равенствозначений в которые входит сомножителем. Подставляя их, получаем следующее уравнение для определения:
 (8.58)
(8.58)
5. Среднее число требований, ожидающих начала обслуживания (средняя длина очереди):
![]()
![]() (8.59)
(8.59)
6. Коэффициент простоя обслуживаемого требования (объекта).
Ранее отмечалось, что СМО можно разбить на две группы - разомкнутые и замкнутые. Типичным представителем систем разомкнутого типа являются предприятие по капитальному ремонту электрических машин, на которое поступают вышедшие из строя электротехнические изделия из многих объектов. Поток отказов электрических машин является случайным, случайным является и объект, из которого поступили заявки.
Замкнутые СМО относятся к классу циклических систем. Для замкнутых СМО характерно конечное число заявок, циркулирующих в системе «источник-СМО». Обслуженные заявки возвращаются в источник и через некоторое время (в общем случае случайное), могут вновь появиться на входе. Поведение источника в замкнутых СМО является некоторой функцией состояния СМО. В связи с этим поток на выходе системы в какой-то мере определяет входящий поток.
Простейшим примером замкнутой СМО может служить работа дежурного электромонтера на объекте, имеющем п электроустановок.
В случае возникновения неисправности электромонтер обслуживает одну электроустановку. Отремонтированное изделие остается на своем рабочем месте и снова становится потенциальным источником на новую заявку, т. е. повторно может выйти из строя и потребовать ремонта. В таких системах, как правило, общее число поступающих заявок ограничено размером объекта и в большинстве случаев является постоянной величиной.
Будем считать, что плотность поступления заявок на обслуживание от электроустановок равна X, число заявок имеет пуассоновское распределение, а время обслуживания распределено по показательному закону с параметром р. В системе могут находиться как обслуженные заявки, так и те, которые стали в очередь и ожидают, пока обслуживаемый канал освободится.
Схема возможных состояний такой системы показана на рис. 1.13.
Рис. 1.13.
Система может иметь следующие состояния:
s 0 - все электроустановки исправны и электромонтер не занят их обслуживанием;
Sj - электромонтер обслуживает одну электроустановку, остальные электроустановки работают;
s 2 - две электроустановки неисправны, одна ремонтируется, вторая находится в очереди;
s k - к электроустановок неисправны, одна ремонтируется, к - 1 стоят в очереди;
s n - п электроустановок неисправны, одна ремонтируется, п - 1 ожидают ремонта.
Стрелки на схеме показывают переходы из одного состояния в другое с интенсивностями X и р.
При переходе системы из состояния s 0 в состояние Sj интенсивность потока неисправностей равна пХ (поток неисправностей всех работающих электроустановок).
При переходе системы из состояния Sj в состояние s 2 интенсивность потока неисправностей уже определяется п - 1 работающими электроустановками (одно изделие находится в ремонте) и т. д.
При переходе же системы по стрелкам справа налево интенсивность потока событий р одинакова (принимается одинаковое время устранения неисправностей в электроустановках).
Такие СМО исследовал К. Пальм, который вывел и получил удобные и простые уравнения для определения вероятностей состояния системы:

Пример 1.15. Дежурный электромонтер на птицефабрике обслуживает 3 объекта. На каждом из объектов в сутки возникает по две неисправности. Процесс устранения неисправности занимает у электромонтера 1 ч. Необходимо рассчитать вероятности состояний, вероятность занятости электромонтера, абсолютную пропускную способность системы.
Пример. С1, С2, С3 – станки; НЦ – центральный накопитель; B – манипулятор. Транспортная тележка (манипулятор) транспортирует отработанную деталь от станка к накопителю и укладывает ее там, забирает новую деталь (заготовку), транспортирует ее к станку и устанавливает в рабочую позицию для зажима. Во время всего периода, необходимого для выгрузки–загрузки, станок простаивает. Время T з смены заготовки и есть время обслуживания.
Интенсивность
обслуживания станков определяется как
,– среднее время обслуживания станка,
которое вычисляется как![]() ,
гдеn
– число заявок. Интенсивность подачи
станком заявки на обслуживание
определяется как
(где–
среднеее время обработки детали станком).
,
гдеn
– число заявок. Интенсивность подачи
станком заявки на обслуживание
определяется как
(где–
среднеее время обработки детали станком).
Станочная система с однозахватным манипулятором представляет собой СМО с ожиданием с внутренней организацией FIFO: каждая заявка станка на обслуживание удовлетворяется, в случае когда манипулятор занят, заявка становится в очередь и станок ожидает когда манипулятор освободится. Данный процесс марковский, т.е. случайная выдача заявки на обслуживание в определенный момент времени t 0 не зависит от предыдущих заявок, т.е. от течения процесса в предшествующий период. Продолжительность исполнения заявки может быть различной и является случайной величиной, не зависящей от числа поданных заявок. Весь процесс не зависит от того, что произошло ранее момента времени t 0 .
В станочной системе число заявок на обслуживание может быть равно 0, 1, 2, ... m , где m – общее число станков. Тогда возможны следующие состояния:
S 0 – все станки работают, манипулятор стоит.
S 1 – все станки, кроме одного, работают, манипулятор обслуживает станок, от которого поступила заявка на смену заготовок.
S 2 – работают m -2 станка, на одном станке идет смена заготовки, другой ожидает.
S 3 – работают m -2 станка, один станок обслуживается манипулятором, два станка ожидают в очереди.
S m – все станки стоят, один обслуживается манипулятором, остальные ожидают очереди исполнения заказа.
Рис.4.6.
Вероятность перехода в состояние S k из одного из возможных состояний S 1 , S 2 , ... S m зависит от случайного поступления заявок на обслуживание и вычисляется как:
p 0 – вероятность того, что все станки работают.
Манипулятор работает при состояниях системы от S 1 до S m . Тогда вероятность его загрузки равна: .
Число
станков, находящихся в очереди связано
с состояниями S
2
,
–
S
m
,
при этом один станок обслуживается, а
(k-1)
– ожидают. Тогда, среднее число станков
в очереди:
 .
.
Коэффициент
простоя одного станка (из-за ожидания
при многостаночном обслуживании):
 .
.
Среднее использование одного станка:
Применение метода Монте-Карло для решения задач, связанных с теорией массового обслуживания
Для того, чтобы описать поток однородных событий, достаточно знать закон распределения моментов времени t 1 , t 2 , ..., t k , ..., в которые поступают события.
Для удобства дальнейших рассмотрений целесообразно от величин t 1 , t 2 , ..., перейти к случайным величинам 1 , 2 , ..., m , ... , таким образом, что:

Случайные величины k являются длинами интервалов времени между последовательными моментами t k .
Совокупность случайных величин i считается заданной, если определена совместная функция распределения: . Обычно рассматриваются только непрерывные случайные величины k , поэтому часто пользуются соответствующей функцией плотности f (z 1 , z 2 ,..., z k ) .
Обычно в теории СМО рассматриваются потоки однородных событий без последействия, для которых случайные величины k независимы. Поэтому . Функцииf i (z i ) при i >1 представляют собой условные функции плотности при условии, что в начальный момент интервала k (i >1) поступила заявка. В отличие от этого функция f 1 (z 1 ) является безусловной функцией плотности, т.к. относительно появления или непоявления заявки в начальный момент времени не делается никаких предположений.
Широкое применение имеют так называемые стационарные потоки, для которых вероятностный режим их во времени не изменяется (т.е. вероятность появления k заявок за промежуток времени (t 0 , t 0 + t ) не зависит от t 0 , а зависит только от t и k ). Для стационарных потоков без последействия имеют место соотношения:
где – плотность стационарного потока.
Поступившая в систему заявка может занимать только свободные линии. Относительно порядка занятия линий могут быть сделаны различные предположения:
а) линии занимаются в порядке их номеров. Линия с большим номером не может быть привлечена к обслуживанию заявки, если имеется свободная линии с меньшим номером;
б) линии занимаются в порядке очереди. Освободившаяся линия поступает в очередь и не начинает обслуживания заявок до израсходования всех ранее освободившихся линий;
в)
линии занимаются в случайном порядке
в соответствии с заданными вероятностями.
Если в момент поступления очередной
заявки имеется n
св
свободных линий, то в простейшем случае
вероятность занять некоторую определенную
линию может быть принята равной
.
В более сложных случаях вероятности
![]() считаются зависящими от номеров линий,
моментов их освобождения и других
параметров.
считаются зависящими от номеров линий,
моментов их освобождения и других
параметров.
Аналогичные предположения можно сделать и относительно порядка принятия заявок к обслуживанию в том случае, когда в системе образуется очередь заявок:
а) заявки принимаются к обслуживанию в порядке очереди. Освободившаяся линия приступает к обслуживанию той заявки, которая ранее другой поступила в систему;
б) заявки принимаются к обслуживанию по минимальному времени получения отказа. Освободившаяся линия приступает к обслуживанию той заявки, которая в кратчайшее время может получить отказ;
в) заявки принимаются к обслуживанию в случайном порядке в соответствии с заданными вероятностями. Если в момент освобождения линии имеется m заявок в очереди, то в простейшем случае вероятность выбрать для обслуживания некоторую определенную заявку может быть принята равной q =1/ m . В более сложных случаях вероятности q 1 , q 2 ,..., q m считаются зависящими от времени пребывания заявки в системе, времени, остающегося до получения отказа и других параметров.
Для решения ряда прикладных задач оказывается необходимым учитывать такой важный фактор, как надежность элементов обслуживающей системы. Будем предполагать, что с точки зрения надежности каждая линия в данный момент времени может быть либо исправной, либо неисправной. Надежность линии определяется вероятностью безотказной работы R = R (t ) , задаваемой как функция времени. Будем также предполагать, что линия, вышедшая из строя по причине неполной надежности, может быть введена в строй (отремонтирована), для чего требуется затратить время p . Величину p будем считать случайной величиной с заданным законом распределения.
Относительно судьбы заявки, при обслуживании которой линия выходит из строя, могут быть сделаны различные предположения: заявка получает отказ; заявка остается в системе (с общим временем пребывания в системе не более n ) как претендент на обслуживание вне очереди; заявка поступает в очередь и обслуживается на общих основаниях и т.д.
Сущность метода статистических испытаний применительно к задачам массового обслуживания состоит в следующем. Строятся алгоритмы, при помощи которых можно вырабатывать случайные реализации заданных потоков однородных событий, а также «моделировать» процессы функционирования обслуживающих систем. Эти алгоритмы используются для многократного воспроизведения реализаций случайного процесса обслуживания при фиксированных условиях задачи. Получаемая при этом информация о состояниях процесса подвергается статистической обработке с целью оценки, являющихся показателями качества обслуживания.
Метод статистических испытаний позволяет более полно, по сравнению с асимптотическими формулами, исследовать зависимость качества обслуживания от характеристик потока заявок и параметров обслуживающей системы.
Это достигается благодаря двум обстоятельствам. Во-первых, при решении задач теории массового обслуживания методом статистических испытаний может быть использована более обширная информация о процессе, чем это обычно удается сделать, применяя аналитические методы.
С другой стороны, значения показателей качества обслуживания, получаемые из асимптотических формул, строго говоря, относятся к моментам времени, достаточно удаленным от начала процесса. Реально, для моментов времени, близких к началу процесса, когда еще не наступил стационарный режим, значения показателей качества обслуживания в общем случае существенно отличаются от асимптотических значений. Метод статистических испытаний позволяет достаточно обстоятельно изучать переходные режимы.
Для многих прикладных задач предположения, при которых справедливы аналитические формулы, оказываются слишком стеснительными. При решении задач методом статистических испытаний некоторые предположения могут быть существенно ослаблены.
В первую очередь это относится к многофазному обслуживанию (т.е. рассматриваются обслуживающие системы, состоящие из нескольких последовательно действующих в общем случае неоднотипных агрегатов).
Другим важным обобщением задачи является предположение о характере потока заявок, поступающих на обслуживание. Допускается рассмотрение потоков однородных событий с практически произвольным законом распределения. Последнее обстоятельство оказывается существенным по следующим двум причинам. Во-первых, реальные потоки заявок в некоторых случаях заметно отличаются от простейшего. Для пояснения второй причины предположим, что исходный поток заявок достаточно точно аппроксимируется простейшим потоком. При этом поток заявок, обслуженных на первой фазе, уже, строго говоря не будет простейшим. Поскольку поток, являющийся выходным для первой фазы, будет входным потоком для агрегата, обслуживающего заявки на второй фазе, мы снова приходим к задаче обслуживания потоков, не являющимися простейшими.
Особенностью замкнутой системы СМО является, то, что длина очереди не ограничивается, так как обслуженные объекты снова могут попадать в систему в виде заявок. Примером такой СМО является зона текущего ремонта АТП, когда автомобиль не может уйти из системы без ремонта. Для замкнутых СМО m→ ∞. В связи с этим формула определения вероятности Р 0 принимает вид
Сумма во втором слагаемом в знаменателе представляет собой геометрическую прогрессию со знаменателем
 . (5.21)
. (5.21)
Известно, что сумма геометрической прогрессии равна
Для установившегося режима (α = const, m→∞) система работает только при условии
 , (5.23)
, (5.23)
то есть когда суммарная пропускная способность всех каналов больше параметра потока заявок. Поэтому указанная сумма представляет собой бесконечно убывающую геометрическую прогрессию и второе слагаемое равно нулю
С учетом этого, вероятность Р 0 определяется по формуле
 (5.25)
(5.25)
При исследовании замкнутых систем решается задача оптимизации каналов обслуживания. Например оптимальным числом постов в зоне ТР будет то, при котором наступает минимум суммарных затрат на создание постов и убытков от простоя автомобилей в ремонте (рис. 5.5)
где m пк - среднее число простаивающих (незанятых каналов); M(S) - средняя длина очереди; а кан - убытки от простоя канала обслуживания в единицу времени; а авт - убытки от простоя автомобиля (потеря прибыли) в единицу времени.

Рис. 5.5. Зависимость удельных затрат на содержание каналов обслуживания (), убытков от простоя в ожидании обслуживания (), и суммарных (), от числа каналов в СМО.
Аналогично применяются оптимальные решения и в других областях, подчиняющихся законам систем массового обслуживания. Оптимизация СМО осуществляется и другими методами, в том числе и с помощью метода статистического моделирования.
Применение ТМО и метода статистического моделирования для определения оптимальных решений
Общие сведения
Метод статистического моделирования (метод Монте-Карло) заключается в воспроизведении исследуемого физического процесса при помощи вероятностной математической модели и вычислении характеристик этого процесса. Он основан на многократных испытаниях построенной модели с последующей статистической обработкой числовых данных для определения статистических оценок параметров процесса. Основой метода статистического моделирования является закон больших чисел.
Под законами больших чисел в теории вероятностей понимается ряд теорем, в которых доказывается сходимость по вероятности статистических характеристик и некоторых постоянных чисел. Так одна из теорем П.Л. Чебышева формулируется так: «При неограниченном увеличении числа независимых испытаний п среднее арифметическое равноточных результатов наблюдений х i случайной величины х , имеющую конечную дисперсию Д [х ], сходится по вероятности к математическому ожиданию М [х ] этой случайной величины.
Теорема Бернулли формулируется так: «При неограниченном увеличении числа независимых испытаний в одних и тех же условиях частость Р(А) наступления события А сходится к его вероятности Р . Поэтому для определения вероятности какого либо события, например вероятности состояний СМО (Р 0 , Р 1 , …Р к ) вычисляются частости для одной реализации, а затем для большого числа реализаций (п =1000). Результат усредняют и с некоторым приближением определяют искомые вероятности состояний системы, математическое ожидание числа занятых каналов, длины очереди и др.
Простейшие потоки событий
Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени. Такой поток можно изобразить как последовательность точек t1...tn на числовой оси, соответствующих случайным моментам появления событий (рис.1.):
Рис.1. Последовательность однородных событий
Поток событий называется стационарным , если вероятность попадания того или иного числа событий на участок времени зависит только от длины этого участка и не зависит от того, где именно на оси 0t расположен этот участок.
Поток событий называется потоком без последействия , если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Поток событий называется ординарным , если вероятности попадания на участок времени малой длины двух или более событий пренебрежимо малы по сравнению с вероятностью попадания на этот участок одного события.
Стационарность потока означает, что вероятностные характеристики этого потока не должны меняться в зависимости от времени. Например, такая характеристика, как интенсивность потока событий, равная математическому ожиданию числа событий в единицу времени, должна оставаться постоянной для стационарного потока.
На практике часто встречаются потоки событий, которые стационарны только на ограниченном участке времени. Например, поток вызовов, поступающих на телефонную станцию в дневное время, может считаться таковым. Тот же поток в течение целых суток уже не будет стационарным, поскольку ночью интенсивность вызовов гораздо меньше, чем днем.
Отсутствие последействия в потоке означает, что события появляются в последовательные моменты времени независимо друг от друга . Например, поток пассажиров, входящих на станцию метро, можно считать потоком без последействия потому, что причины, обусловившие приход отдельного пассажира именно в тот, а не другой момент, не связаны с аналогичными причинами для других пассажиров. Однако условие отсутствия последействия может быть нарушено за счет появления такой зависимости. Например, поток пассажиров, покидающих станцию метро, уже не может считаться потоком без последействия, так как моменты выхода пассажиров, прибывших одним и тем же поездом, зависимы между собой.
Ординарность потока означает, что события в потоке приходят поодиночке , а не парами, тройками и т. д. Например, поток клиентов, направляющихся в парикмахерскую, практически можно считать ординарным, чего нельзя сказать о потоке клиентов, идущих в ЗАГС для регистрации брака.
Простейший поток играет среди потоков событий особую роль, до некоторой степени аналогичную роли нормального закона среди других законов распределения. Согласно центральной предельной теореме, при суммировании большого числа независимых случайных величин, подчиненных практически любым законам распределения, получается случайная величина, приближенно распределенная по нормальному закону. Аналогично можно сказать, что при суммировании (взаимном наложении) большого числа ординарных, стационарных потоков с практически любым последействием получается поток, сколь угодно близкий к простейшему . Условия, которые должны для этого соблюдаться, аналогичны условиям центральной предельной теоремы, а именно: складываемые потоки должны оказывать на сумму приблизительно равномерно малое влияние.
Замкнутые системы массового обслуживания
Рассмотрим системы массового обслуживания, в которых интенсивность потока поступающих заявок зависит от состояния самих систем. Такие системы массового обслуживания называются замкнутыми .
Пусть система состоит из п каналов обслуживания и т источников заявок, т>п.
Предположим, что каждый источник порождает простейший поток заявок с интенсивностью , причем источник не может посылать следующую заявку до завершения обслуживания своей предыдущей заявки (в этом и выражается замкнутость данной системы). Предположим также, что каждый канал порождает простейший поток обслуженных заявок с интенсивностью . Все состояния данной системы можно разбить условно на три группы:
- "все каналы свободны",
- "ровно i каналов занято и поступило ровно i заявок", i = 1, ..., n ,
- "все каналы заняты и ровно j-n заявок находятся в очереди для обслуживания", j = n + 1, ..., m.
Графически все возможные переходы из состояния в состояние, а также интенсивности потоков событий, под воздействием которых эти переходы возможны, можно изобразить в виде размеченного графа так, как это показано на рис.2. Действительно, если система находится в состоянии i = 0, 1,..., n - 1, то в состояние "i + 1 каналов занято" она может перейти под воздействием суммарного потока заявок от m - i источников с интенсивностью ; из состояния в состояние "i - 1 каналов занято" она может перейти под воздействием суммарного потока обслуженных заявок, поступающего от i каналов обслуживания с интенсивностью .. Напомним, что i источников прекращают поставку заявок до завершения обслуживания своих последних заявок. Если же система находится в состоянии , j = n,...,m- 1, то в состояние она может перейти под воздействием суммарного потока заявок с интенсивностью , а в состояние - под воздействием суммарного потока обслуженных заявок с интенсивностью , поступающего от n каналов обслуживания.