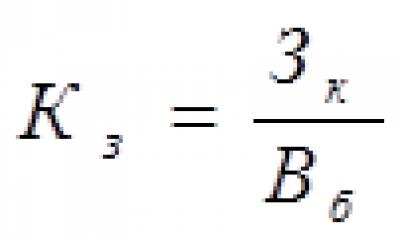Вариация - это несовпадение значений одной и той же статистической величины у разных объектов в силу особенностей их собственного развития, а также различия условий, в которых они находятся. Вариация имеет объективный характер и помогает познать сущность изучаемого явления. Если средняя величина сглаживает индивидуальные различия, то вариация, наоборот, их подчеркивает, устанавливая типичность или не типичность найденной средней величины для конкретной статистической совокупности. Тем самым можно делать вывод о качественности подобранных статистических данных.

Вариация измеряется с помощью относительных величин, называемых коэффициентами вариации и определяемых в виде отношения среднего отклонения к средней величине. Поскольку среднее отклонение может определяться линейным и квадратическим способами, то соответствующими могут быть и коэффициенты вариации. Следовательно, коэффициенты вариации надо определять по формулам

– линейный; (1.28)

– квадратический. (1.29) Значения коэффициента вариации изменяются от 0 до 1 и чем ближе он к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности, а значит и качественнее подобраны статистические данные. При этом критериальным значением коэффициента вариации служит 1/3.

То есть средняя величина считается типичной для данной совокупности при λ 0,333 или при ν 0,333. В ином случае средняя величина не типична и требуется пересмотреть статистическую совокупность с целью включения в нее более объективных статистических величин.

Обычно квадратический коэффициент вариации несколько (примерно на 25%) больше линейного, рассчитанные по одним и тем же данным. А значит возможен случай, когда λ 0,333 и ν 0,333, тогда необходимо взять среднюю из этих коэффициентов и по ее значению сделать окончательный вывод о не/типичности найденной средней величины.

С помощью линейного коэффициента вариации принципиальный вывод о типичности или не типичности средней величины можно получить проще и быстрее, чем с помощью квадратического. Однако квадратический коэффициент применяется чаще, так как существует несколько способов для вычисления дисперсии.

У такого способа оценки вариации есть и существенный недостаток. Действительно, пусть, например, исходная совокупность рабочих, имеющих средний стаж 15 лет, со стандартным отклонением σ = 10 лет, «состарилась» еще на 15 лет. Теперь= 30 лет, а стандартное отклонение по-прежнему равно 10. Совокупность, ранее бывшая неоднородной (10/15*100 = 66,7%), со временем оказывается, таким образом, вполне однородной (10/30*100 = 33,3 %).

Поэтому возможен дополнительный анализ статистической совокупности с помощью коэффициента осцилляции , определяемого по формуле

где R - размах вариации в виде разности наибольшего и наименьшего значений в совокупности статистических величин. То есть

R = Хмах –Хmin, (1.31)

где Xмax и Xmin - максимальное и минимальное значения в совокупности.

При упорядочении статистических величин в совокупности образуются группировочные интервалы. Тогда под обозначением ∆Х понимается размах интервала, а среднее интервальное значение обозначается ХИ . В случае ориентировки только на квадратический коэффициент вариации могут применяться разные методы определения дисперсии.

Полученные из опыта величины неизбежно содержат погрешности, обусловленные самыми разнообразными причинами. Среди них следует различать погрешности систематические и случайные. Систематические ошибки обусловливаются причинами, действующими вполне определенным образом, и могут быть всегда устранены или достаточно точно учтены. Случайные ошибки вызываются весьма большим числом отдельных причин, не поддающихся точному учету и действующих в каждом отдельном измерении различным образом. Эти ошибки невозможно совершенно исключить; учесть же их можно только в среднем, для чего необходимо знать законы, которым подчиняются случайные ошибки.

Будем обозначать измеряемую величину через А, а случайную ошибку при измерении х. Так как ошибка х может принимать любые значения, то она является непрерывной случайной величиной, которая вполне характеризуется своим законом распределения.

Наиболее простым и достаточно точно отображающим действительность (в подавляющем большинстве случаев) является так называемый нормальный закон распределения ошибок :

Этот закон распределения может быть получен из различных теоретических предпосылок, в частности, из требования, чтобы наиболее вероятным значением неизвестной величины, для которой непосредственным измерением получен ряд значений с одинаковой степенью точности, являлось среднее арифметическое этих значений. Величина 2 называется дисперсией данного нормального закона.

Среднее арифметическое

Определение дисперсии по опытным данным. Если для какой-либо величины А непосредственным измерением получено n значений a i с одинаковой степенью точности и если ошибки величины А подчинены нормальному закону распределения, то наиболее вероятным значением А будет среднее арифметическое :

a - среднее арифметическое,

a i - измеренное значение на i-м шаге.

Отклонение наблюдаемого значения (для каждого наблюдения) a i величины А от среднего арифметического : a i - a.

Для определения дисперсии нормального закона распределения ошибок в этом случае пользуются формулой:

2 - дисперсия,
a - среднее арифметическое,
n - число измерений параметра,

Среднеквадратическое отклонение

Среднеквадратическое отклонение показывает абсолютное отклонение измеренных значений от среднеарифметического . В соответствии с формулой для меры точности линейной комбинации средняя квадратическая ошибка среднего арифметического определяется по формуле:

, где

a - среднее арифметическое,
n - число измерений параметра,
a i - измеренное значение на i-м шаге.

Коэффициент вариации

Коэффициент вариации характеризует относительную меру отклонения измеренных значений от среднеарифметического :

, где

V - коэффициент вариации,
- среднеквадратическое отклонение,
a - среднее арифметическое.

Чем больше значение коэффициента вариации , тем относительно больший разброс и меньшая выравненность исследуемых значений. Если коэффициент вариации меньше 10%, то изменчивость вариационного ряда принято считать незначительной, от 10% до 20% относится к средней, больше 20% и меньше 33% к значительной и если коэффициент вариации превышает 33%, то это говорит о неоднородности информации и необходимости исключения самых больших и самых маленьких значений.

Среднее линейное отклонение

Один из показателей размаха и интенсивности вариации - среднее линейное отклонение (средний модуль отклонения) от среднего арифметического. Среднее линейное отклонение рассчитывается по формуле:

, где

_
a - среднее линейное отклонение,
a - среднее арифметическое,
n - число измерений параметра,
a i - измеренное значение на i-м шаге.

Показатель асимметрии

Показатель асимметрии (A) и его ошибка (m a) рассчитывается по следующим формулам:

, где

А - показатель асимметрии,
- среднеквадратическое отклонение,
a - среднее арифметическое,
n - число измерений параметра,
a i - измеренное значение на i-м шаге.

Показатель эксцесса

Показатель эксцесса (E) и его ошибка (m e) рассчитывается по следующим формулам:

, где

Коэффициент вариации – это один из наиболее применимых в финансовой сфере статистических коэффициентов. Расскажем, как рассчитать коэффициент вариации и чем он может пригодиться финансовому директору.

Что такое коэффициента вариации и зачем он нужен

Коэффициент вариации (Coefficient of variation, или CV) – это мера относительного разброса случайной величины. Он показывает, какую долю составляет средний разброс случайной величины от среднего значения этой величины.

В общем случае коэффициент вариации используют для определения дисперсии значений без привязки к масштабу измеряемой величины и единицам измерения. Коэффициент вариации входит в группу относительных методов статистики, измеряется в процентах и поэтому его можно использовать для сравнения вариации нескольких не связанных между собой процессов и явлений.

Использование коэффициента вариации в финансовом моделировании

Коэффициент вариации является лидером среди вариационных статистических методов, которые используют финансовые и инвестиционные аналитики.

Аналитики используют коэффициент:

Для определения устойчивости прогнозной модели.
Для сравнения нескольких прогнозных моделей (в основном инвестиционных) с разными абсолютными уровнями дохода и риска.
Для проведения XYZ анализа.

Формула расчета коэффициента вариации

Коэффициент вариации рассчитывается по формуле:

где CV – коэфф вариации,

σ – среднеквадратическое отклонение случайной величины,

tср – среднее значение случайной величины.

Формула коэффициента вариации для инвестиционных финансовых моделей:

где NPV – чистый приведенный доход.

Формула коэффициента вариации для инвестиций в ценные бумаги:

где:%год – доходность по ценной бумаге в % годовых.

Коэффициент вариации в Excel

=СТАНДОТКЛОНПА(диапазон значений)/СРЗНАЧ (диапазон значений)

Или с использованием встроенного пакета «Анализ данных».

Анализ коэффициента вариации

Коэффициент вариации более универсален, в отличие от дисперсии и среднеквадратического отклонения, потому что позволяет сопоставлять риск и доходность двух и более активов, которые могут существенно отличаться. Правда, у метода оценки пары доходность/риск с помощью коэффициента вариации есть ограничения. Если ожидаемая доходность стремится к нулю, то значение коэффициента вариации стремится к бесконечности. И даже незначительное изменение ожидаемой доходности проекта (или ценной бумаги) приводит к значительному изменению коэффициента, что необходимо учитывать при обосновании инвестиционных решений.

меньше 10%, то степень риска проекта является незначительной,
от 10% до 20% – средней,
больше 20% – значительной,
если значение коэффициента вариации больше 33%, то финансовая модель считается неоднородной, неустойчивой. По ней нельзя принимать объективных инвестиционных решений

Примеры расчета коэффициента вариации в Excel

Пример 1

Первый – открытие сети розничных точек для торговли ювелирными изделиями в Москве и Санкт-Петербурге.

Второй – открытие сети розничных точек по всей России в городах-миллионниках.

Финансовый аналитик предприятия составил финансовые модели обоих проектов в Excel и по модели Монте-Карло сделал по 5000 прогонов для NPV в каждом проекте (см. также, как создать наглядную финансовую модель в Excel ). Далее с помощью пакета анализа «Анализ данных» получил следующие статистические показатели (см. таблицы 1 и 2).

Таблица 1 . Показатели по проекту 1

Средний предполагаемый NPV от Проекта 1 составит 14,05 тысяч долларов, дисперсия (она же среднее квадратическое отклонение) будет равна 1,72 тысяч долларов.

Коэффициент вариации для первого проекта равен:

CV = 1.72/14.05 = 12%

Проект признается среднерисковым.

Средний предполагаемый NPV от Проекта 2 составит 25,23 тысяч долларов, дисперсия будет равна 6,30 тысяч долларов.

Коэффициент вариации для второго проекта составит:

CV = 6,30/25,23 = 24,97%

Проект признается высокорисковым.

Если сравнивать проекты 1 и 2 по коэффициенту вариации, то следует выбрать Проект 1, так как соотношение доход/риск у него лучше.

Пример 2

Компания «Сигма» проводит XYZ анализ товарного ассортимента по показателю изменчивости продаж. Продуктовая линейка компании представлена пятью товарами: А, В, С, D и E.

Имеется помесячная статистика продаж за последний год по каждому товару (см. рисунок). На практике лучше иметь статистику за период более трех лет/

Рисунок . Статистика продаж за последний год по каждому товару

Финансовый аналитик компании рассчитал коэффициент вариации для каждого товара

CVа = СТАНДОТКЛОНПА(B2:В13)/СРЗНАЧ (В2:В13) = 30%

В компании установлены следующие интервалы для групп XYZ:

Z – 31–100%.

Значит, товары B и D относятся к категории X. Спрос на них постоянный, запасы на складах по ним должны быть под пристальным контролем и постоянно пополняться.

Товары A и C относятся к категории Y. Спрос на них отклоняется в пределах 30% от месяца к месяцу. Возможно, имеет место сезонность спроса. Нужно глубже анализировать статистику продаж и выработать оптимальную политику по остаткам на складах для данной группы.

Товар E имеет наиболее волатильный спрос, продажи по нему осуществляются нерегулярно, поэтому возможно имеет смысл перейти на работу с ним по предзаказу.

Выводы

Следует помнить, что коэффициент вариации – это не единственный способ оценки эффективности инвестирования, так как он не учитывает несколько важных факторов:

Объемы первоначального инвестирования.
Возможную асимметричность распределения. При расчете коэффициента вариации предполагается, что разброс значений случайной величины расположен симметрично к среднему (часто по нормальному распределению). Но это не всегда соответствует действительности. Например, для опционов, доходность которых не может быть ниже нуля, имеет место асимметрия распределения, и анализировать коэффициент вариации по ним нужно с оглядкой на другие методы статистического анализа.
Инвестиционную политику субъекта инвестирования.
Другие нечисловые факторы.

Однако метод оценки статистических, в том числе финансовых, данных посредством расчета коэффициента вариации заслуженно признан одним из наиболее эффективных сравнительных методов статистики.

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

Показатели описательной статистики

Существует несколько показателей, которые использует описательная статистика.

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

Ширина интервала, куда попадает рост всех студентов, – 18 см.
В распределении рост наиболее близок к середине этого интервала.
Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться. Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического. Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Если свести все к строгим математическим терминам, то определение среднего арифметического (обозначается греческой буквой – μ («мю»)) будет звучать так:

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ 2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Среднее квадратичное отклонение хорошо работает с рядами, в которых разброс значений не очень велик (это хорошо прослеживалось на примере роста, где интервал был всего 18 см). Если бы ряд наших измерений был значительнее, а варьирование роста было сильнее, то стандартное отклонение стало непоказательным и нам потребовался бы критерий, который может отразить разброс в относительных единицах (т. е. в процентах, относительно средней величины).

Для этих целей предусмотрены абсолютные и относительные показатели вариации в статистике, характеризующие вариационные масштабы:

Размах вариации.

Квадратический коэффициент вариации (обозначается как Vσ) – это отношение среднеквадратичного отклонения к среднеарифметическому значению, выраженное в процентах.

Для нашего примера со студентами, определить Vσ несложно - он будет равен 3,18%. Основная закономерность – чем больше будет изменяться значение коэффициента, тем больше разброс вокруг среднего значения и тем менее однородна выборка.

Преимущество коэффициента вариации в том, что он показывает однородность значений (асимметрия) в ряду наших измерений, кроме того, на него не оказывают влияния масштаб и единицы измерения. Эти факторы делают коэффициент вариации особенно популярным в биомедицинских исследованиях. Будет считаться , что эксцесс значения Vσ =33% отделяет однородные выборки от неоднородных.

Если найти в ряду значений роста (первый пример) максимальное и минимальное значения, то получим размах вариации (обозначается как R, иногда ещё называется колеблемостью). В нашем примере – это значение будет равно 18 см. Эта характеристика используется для расчёта коэффициента осцилляции:

Коэффициент осцилляции – показывает как размах вариации будет относиться к среднему арифметическому ряда в процентном отношении.

Расчёты в Microsoft Ecxel 2016

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию :

Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
Дисперсия – это среднее значение отклонений возведенное в квадрат.
Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

В этом же документе приводятся правила определения коэффициента вариации. Разработано несколько методик выявления НМЦК: нормативная, тарифная, проектно-сметная, затратная. Самым приоритетным считается метод сопоставимых рыночных цен. Именно его рекомендуется использовать при определении стартовой цены. Он предполагает сравнение коммерческих предложений, предоставляемых потенциальными поставщиками по запросу заказчика. Для проведения такого анализа и применяется коэффициент вариации. Он выражается в процентах. Под коэффициентом вариации понимается мера относительного разброса предлагаемых цен. Он показывает, какую долю занимает средний разброс цен от среднего значения цены. Этот показатель может принимать следующие значения:

Меньше 10%. В таком случае разница в ценах признается незначительной.
От 10% до 20%. Разброс считается средним.
От 20% до 33%.

Коэффициент вариации

Для проверки соответствия исследуемых значений закону нормального распределения применяют отношение показателя асимметрии к его ошибке и отношение показателя эксцесса к его ошибке. Показатель асимметрии Показатель асимметрии (A) и его ошибка (ma) рассчитывается по следующим формулам: , где А — показатель асимметрии, — среднеквадратическое отклонение,a — среднее арифметическое,n — число измерений параметра,ai — измеренное значение на i-м шаге.

Показатель эксцесса Показатель эксцесса (E) и его ошибка (me) рассчитывается по следующим формулам: , где Е — показатель эксцесса, — среднеквадратическое отклонение,a — среднее арифметическое,n — число измерений параметра,ai — измеренное значение на i-м шаге. Если А < 0, то больше данных с меньшими значениями, чем среднеарифметическое.
Если Е < 0, то данные сконцентрированы около среднеарифметического значения.

Инфо

X – отдельные значения, X̅– среднее арифметическое по выборке. Примечание. Для расчета дисперсии в Excel предусмотрена специальная функция.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. В то же время не все так плохо.
При увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной. Поэтому при работе с большими размерами выборок можно использовать формулу выше.
Язык знаков полезно перевести на язык слов. Получится, что дисперсия — это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности.

Что характеризует коэффициент вариации

Для определения дисперсии нормального закона распределения ошибок в этом случае пользуются формулой: , где 2 — дисперсия,a — среднее арифметическое,n — число измерений параметра,ai — измеренное значение на i-м шаге. Среднеквадратическое отклонение Среднеквадратическое отклонение показывает абсолютное отклонение измеренных значений от среднеарифметического.
В соответствии с формулой для меры точности линейной комбинации средняя квадратическая ошибка среднего арифметического определяется по формуле: , где — среднеквадратическое отклонение,a — среднее арифметическое,n — число измерений параметра,ai — измеренное значение на i-м шаге. Коэффициент вариации Коэффициент вариации характеризует относительную меру отклонения измеренных значений от среднеарифметического: , где V — коэффициент вариации, — среднеквадратическое отклонение,a — среднее арифметическое.

Вариация (статистика)

Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением. На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N).

В виде формулы это рассчитывается понятнее: Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример: Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии.

Коэффициент вариации в статистике: примеры расчета

Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, мы просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя.

Внимание

Разгадка заключается всего в трех словах. Однако в чистом виде, как, например, средняя арифметическая, или индекс, дисперсия не используется. Это скорее вспомогательный и промежуточный показатель, который необходим для других видов статистического анализа.

У нее даже единицы измерения нормальной нет. Судя по формуле, это квадрат единицы измерения исходных данных. Без бутылки, как говорится, не разберешься.

Статистические параметры

Было получено четыре коммерческих предложения цен: 2500 рублей, 2800 рублей, 2450 рублей и 2600 рублей. В первую очередь необходимо рассчитать среднеарифметическое значение цены Следующим шагом становится расчет среднеквадратичного отклонения Осталось только рассчитать коэффициент вариации Полученное значение коэффициента меньше 33%, следовательно, все собранные данные подходят для расчета стартовой цены контракта. Расчет НМЦК и коэффициента вариации оформляются в форме отчета, который становится обязательной частью закупочной документации. Коэффициент вариации – важный инструмент, позволяющий оценить правильность ценовых предложений, полученных от поставщиков. Поэтому при составлении документации заказчикам необходимо учитывать правила расчета этого показателя и особенности его применения.